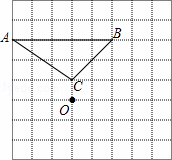
如图，已知△ABC和点O．
（1）把△ABC绕点O顺时针旋转90°得到△A1B1C1，在网格中画出△A1B1C1；
（2）用直尺和圆规作△ABC的边AB，AC的垂直平分线，并标出两条垂直平分线的交点P（要求保留作图痕迹，不写作法）；指出点P是△ABC的内心，外心，还是重心？
科目：初中数学 来源： 题型：
一农妇在市场卖葱，当时市场上的葱价是1.00元一斤，一葱贩对农妇说：“我想把你的葱分开来买，葱叶0.50元一斤，葱白0.50元一斤．”农妇听了葱贩的话，不假思索就把葱全部卖完．当农妇数过钱之后才发现只卖了一半钱。此时葱贩已不见踪影．聪明的你，请运用数学语言揭穿葱贩的把戏．
过程如下：设总量z斤，葱叶x斤，葱白y斤，列方程
∵x+y=z，∴卖给葱贩的钱为0.5x+0.5y=0.5z，
而实际应卖的钱为1.0x+1.0y=1.0z，结果一目了然，那葱贩只用了一半钱就买了所有葱．
生活常识告诉我们，人们在吃葱的时候主要吃的是葱白，葱白应比葱叶卖的贵．
假设一根葱的葱叶和葱白重量相同，葱叶和葱白的价钱之和仍是1.00元．请用数学语言说明此时农妇还是只卖了一半的钱．
假设一根葱的葱叶和葱白重量不同，且葱叶的重量大于葱白的重量，葱叶0.20元一斤，葱白0.80元一斤．请用数学语言说明此时农妇卖的钱少于一半．
查看答案和解析>>
科目：初中数学 来源： 题型：
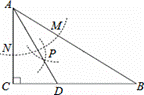
如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法中正确的个数是（ ）
①AD是∠BAC的平分线；②∠ADC=60°；
③点D在AB的中垂线上；④S△DAC：S△ABC=1：3
A.1 B.2 C.3 D.4
查看答案和解析>>
科目：初中数学 来源： 题型：
若正整数n使得在计算n+（n+1）+（n+2）的过程中，个数位上均不产生进位现象，则称n为“本位数”，例如2和30是 “本位数”，而5和91不是“本位数”.现从所有大于0且小于100的“本位数”中，随机抽取一个数，抽到奇数的概率为____。
查看答案和解析>>
科目：初中数学 来源： 题型：
我国“神州八号飞船”顺利升空，如果飞船发射前10秒记为—10秒，那么飞船发射后15秒
记为（ ）
A．—10秒 B．＋10秒 C．—15秒 D．＋15秒
查看答案和解析>>
科目：初中数学 来源： 题型：
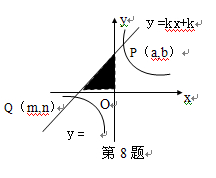
如图，一次函数ｙ=kx+k的图象与两坐标轴围成的三角形（阴影部分）
的面积是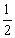
，与反比例函数ｙ=
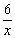的图形相交于点P（a,b）和Q（m，
n），则（a+m）—（n+b）+ mn的值是（ ）
A．—4 B．4 C．—6 D．6
查看答案和解析>>
科目：初中数学 来源： 题型：
如果一条抛物线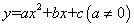
与
轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线三角形系数”.
（1）若抛物线三角形系数为[-1,b,0]的“抛物线三角形”是等腰直角三角形，求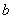
的值；
（2）若△OAB是“抛物线三角形”，其中点B为顶点，抛物线三角形系数为[-2，2m，0]，其中m＞0；且四边形ABCD是以原点O为对称中心的矩形，求出过O、C、D三个点的抛物线的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
圆周的一个扇形，将留下的扇形围成一个圆锥的侧面（接缝处不重叠），那么这个圆锥的高为 cm．
、
分别是方程
的两根，两圆的圆心距为5，则两圆的位置关系是（ ）