
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则以下结论中:①F为CD的中点;②3AM=2DE;③tan∠EAF=![]() ;④
;④![]() ;⑤△PMN∽△DPE,正确的结论个数是( )
;⑤△PMN∽△DPE,正确的结论个数是( )
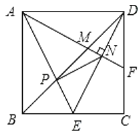
A.1个B.2个C.3个D.4个
【答案】D
【解析】
逐个结论进行判断:
①证明△ECD≌△FDA(AAS),即可得出结论F为CD的中点;
②根据△ABM和△FDM组成的沙漏模型,利用相似三角形对应线段成比例即可判断;
③在Rt△ANE中,tan∠EAF=![]() ,在△ADE和△ADF中分别运用面积法求出AN,DN,运用勾股定理求出DE,则EN=DE-EN,据此计算判断;
,在△ADE和△ADF中分别运用面积法求出AN,DN,运用勾股定理求出DE,则EN=DE-EN,据此计算判断;
④作PH⊥AF于H,通过构造直角三角形,运用相似模型和勾股定理求出PN;
⑤由PN≠DN,推出对应角不相等,即可得出结论.
①F为CD的中点;
∵ABCD是正方形
∴AB=BC=AD=CD=2,∠FDA=∠ECD=90°
∵AF⊥DE
∴∠CDE+∠AFD=90°
又∵∠CDE+∠DEC=90°
∴∠AFD=∠DEC
∴△ECD≌△FDA(AAS)
∴DF=CE
∵E是BC的中点
∴F是CD的中点
故结论①正确;
②3AM=2DE;
∵AB∥DC
∴![]()
∴![]()
由①知:AF=DE
∴3AM=2DE
故结论②正确.
③tan∠EAF=![]() ;
;
由勾股定理得:
AF=DE=AE=![]()
∵S△ADE=![]() ×2×2=
×2×2=![]() ×
×![]() ×AN
×AN
∴AN=![]()
∵S△ADF=![]() ×2×1=
×2×1=![]() ×
×![]() ×DN
×DN
∴DN=![]()
∴EN=DE-DN=![]()
![]() =
=![]()
∴tan∠EAF=![]() =
=![]()
![]()
故结论③正确.
④![]() ;
;
如图,作PH⊥AN于H
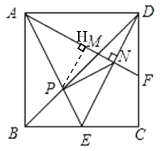
∵AD∥BE
∴![]()
∴![]()
∵FH∥EN
∴![]()
∴AH=![]() ,PH=
,PH=![]()
∴NH=![]()
由勾股定理得:
![]()
故结论④正确.
⑤△PMN∽△DPE
∵PN≠DN
∴∠MPN≠∠PDE
∴△PMN与△DPE不相似
故结论⑤错误.
所以正确结论为①②③④.
故选:D


科目:初中数学 来源: 题型:
【题目】綦江区某中学的国旗护卫队需从甲、乙两队中选择一队身高比较整齐的队员担任护旗手,每队中每个队员的身高(单位:cm)如下:
甲队 | 178 | 177 | 179 | 179 | 178 | 178 | 177 | 178 | 177 | 179 |
乙队:

分析数据:两组样本数据的平均数、中位数、众数、方差如下表所示:
整理、描述数据:
平均数 | 中位数 | 众数 | 方差 | |
甲队 | 178 | 178 | b | 0.6 |
乙队 | 178 | a | 178 | c |
(1)表中a=______,b=______,c=______;
(2)根据表格中的数据,你认为选择哪个队比较好?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,平行四边形
为坐标原点,平行四边形![]() 的边
的边![]() 在
在![]() 轴正半轴上,顶点
轴正半轴上,顶点![]() 在
在![]() 轴正半轴上,函数
轴正半轴上,函数![]() 的图像经过点
的图像经过点![]() ,点
,点![]() 是线段
是线段![]() 上接近点
上接近点![]() 的三等分点,
的三等分点,![]() ,垂足为点
,垂足为点![]() ,且
,且![]() 恰好是线段
恰好是线段![]() 的中点,连结
的中点,连结![]() ,
,![]() 交于点
交于点![]() ,则四边形
,则四边形![]() 的面积是()
的面积是()
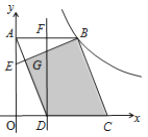
A.![]() B.5C.
B.5C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳出行,绿色出行”,自行车逐渐成为人们喜爱的交通工具,宁波某运动商城的自行车销售量自2016年起逐年增加,据统计该商城2016年销售自行车768辆,2018年销售了1200辆.
(1)若该商城近四年的自行车销售量年平均增长率相同,请你预估:该商城2019年大概能卖出多少辆自行车?
(2)考虑到自行车需求的不断增加,本月该商场准备投入3万元再购进一批两种规格的自行车,已知![]() 型车的进价为500元/辆,售价为700元/辆,
型车的进价为500元/辆,售价为700元/辆,![]() 型车的进价为1000元/辆,售价为1300元/辆.根据销售经验,
型车的进价为1000元/辆,售价为1300元/辆.根据销售经验,![]() 型车不少于
型车不少于![]() 型车的2倍,但不超过
型车的2倍,但不超过![]() 型车的3.2倍,假设所进车辆全部售完,为使得利润最大,该商场该如何进货?
型车的3.2倍,假设所进车辆全部售完,为使得利润最大,该商场该如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“脐橙结硕果,香飘引客来”,赣南脐橙以其“外表光洁美观,肉质脆嫩,风味浓甜芳香”的特点饮誉中外.现欲将一批脐橙运往外地销售,若用2辆A型车和1辆B型车载满脐橙一次可运走10吨;用1辆A型车和2辆B型车载满脐橙一次可运走11吨.现有脐橙31吨,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满脐橙.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都载满脐橙一次可分别运送多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若1辆A型车需租金100元/次,1辆B型车需租金120元/次.请选出费用最少的租车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
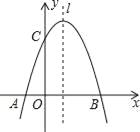
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
正方形内“奇妙点”及性质探究
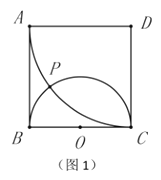
定义:如图1,在正方形![]() 中,以
中,以![]() 为直径作半圆
为直径作半圆![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,与半圆
,与半圆![]() 交于点
交于点![]() .我们称点
.我们称点![]() 为正方形
为正方形![]() 的一个“奇妙点”.过奇妙点的多条线段与正方形
的一个“奇妙点”.过奇妙点的多条线段与正方形![]() 无论是位置关系还是数量关系,都具有不少优美的性质值得探究.
无论是位置关系还是数量关系,都具有不少优美的性质值得探究.
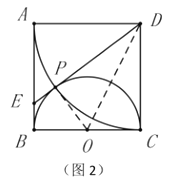
性质探究:如图2,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,则
,则![]() 为半圆
为半圆![]() 的切线.
的切线.
证明:连接![]() .
.
由作图可知,![]() ,
,
又![]() .
.
![]()
![]() ,∴
,∴![]() 是半圆
是半圆![]() 的切线.
的切线.
问题解决:
(1)如图3,在图2的基础上,连接![]() .请判断
.请判断![]() 和
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
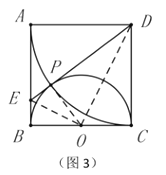
(2)在(1)的条件下,请直接写出线段![]() 之间的数量关系;
之间的数量关系;
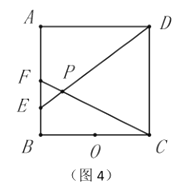
(3)如图4,已知点![]() 为正方形
为正方形![]() 的一个“奇妙点”,点
的一个“奇妙点”,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,请写出
,请写出![]() 和
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
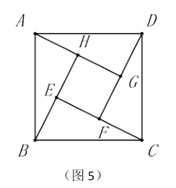
(4)如图5,已知点![]() 为正方形
为正方形![]() 的四个“奇妙点”.连接
的四个“奇妙点”.连接![]() ,恰好得到一个特殊的“赵爽弦图”.请根据图形,探究并直接写出一个不全等的几何图形面积之间的数量关系.
,恰好得到一个特殊的“赵爽弦图”.请根据图形,探究并直接写出一个不全等的几何图形面积之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
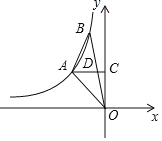
【题目】如图,A、B是反比例函数![]() 图象上的两点,过点A作AC⊥y轴,垂足为C,交OB于点D,且D为OB的中点,若△ABO的面积为4,则k的值为______.
图象上的两点,过点A作AC⊥y轴,垂足为C,交OB于点D,且D为OB的中点,若△ABO的面积为4,则k的值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com