
【题目】填写证明的理由.
已知:如图,AB∥CD,EF、CG分别是∠AEC、∠ECD的角平分线;求证:EF∥CG.
证明:∵AB∥CD(已知)
∴∠AEC=∠DCE ()
又∵EF平分∠AEC (已知)
∴∠1= ![]() ∠AEC ()
∠AEC ()
同理∠2= ![]() ∠DCE,∴∠1=∠2
∠DCE,∴∠1=∠2
∴EF∥CG ()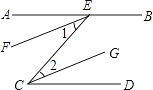
【答案】两直线平行,内错角相等;角平分线的定义;内错角相等,两直线平行
【解析】证明:∵AB∥CD(已知),
∴∠AEC=∠DCE (两直线平行,内错角相等);
又∵EF平分∠AEC(已知),
∴∠1= ![]() ∠AEC(角平分线的定义),
∠AEC(角平分线的定义),
同理∠2= ![]() ∠DCE,
∠DCE,
∴∠1=∠2,
∴EF∥CG (内错角相等,两直线平行).
【考点精析】本题主要考查了角的平分线和平行线的判定与性质的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.


科目:初中数学 来源: 题型:
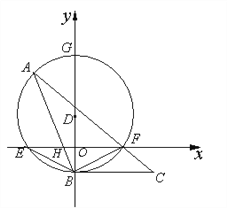
【题目】如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在![]() 上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
上,连接AB交x轴于点H,连接 AF并延长到点C,使∠FBC=∠A.
(1)判断直线BC与⊙D的位置关系,并说明理由;
(2)求证:BE2=BH·AB;
(3) 若点E坐标为(-4,0),点B的坐标为(0,-2),AB=8,求F与A两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
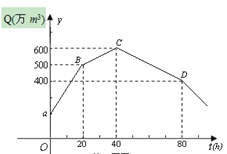
【题目】因长期干旱,甲水库蓄水量降到了正常水位的最低值,为灌溉需要,由乙水库向甲水库匀速供水,20h后,甲水库打开一个排灌闸为农田匀速灌溉,又经过20h,甲水库打开另一个排灌闸同时灌溉,再经过40h,乙水库停止供水.甲水库每个排灌闸的灌溉速度相同,图中的折线表示甲水库蓄水量Q(万m3)与时间t(h)之间的函数关系.
求: (1)线段BC的函数表达式;
(2)乙水库供水速度和甲水库一个排灌闸的灌溉速度;
(3)乙水库停止供水后,经过多长时间甲水库蓄水量又降到了正常水位的最低值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°
(1)如图1,当点A、C、D在同一条直线上时,AC=12,EC=5
①求证:AF⊥BD ②求AF的长度;
(2)如图2,当点A、C、D不在同一条直线上时,求证:AF⊥BD; 
(3)如图3,在(2)的条件下,连接CF并延长CF交AD于点G,∠AFG是一个固定的值吗?若是,求出∠AFG的度数;若不是,请说明理由 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com