
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 分析四个给定函数,根据函数的系数结合函数的性质,找出其在定义域内的单调性,由此即可得出结论.
解答 解:①在反比例函数y=-$\frac{2}{x}$(x>0)中,k=-2,
∴该函数在x>0中单调递增;
②在一次函数y=-2x+1中,k=-2,
∴该函数在其定义域内单调递减;
③二次函数y=3x2+1(x<0)中a=3>0,且对称轴为x=0,
∴该函数在x<0中单调递减;
④一次函数y=x+3中,k=1,
∴该函数在其定义域内单调递增.
综上可知:y随x的增大而减小的函数有②③.
故选B.
点评 本题考查了反比例函数的性质、一次函数的性质以及二次函数的性质,解题的关键是结合函数的系数找出函数的单调性.本题属于基础题,难度不大,解决该题型题目时,根据函数的系数结合函数的性质找出函数的单调性是关键.


科目:初中数学 来源: 题型:选择题
| 每天使用零花钱(单位:元) | 0 | 1 | 2 | 3 | 4 | 5 |
| 人数 | 2 | 5 | 6 | 4 | 2 | 1 |
| A. | 众数是2元 | B. | 中位数是2元 | C. | 极差是5元 | D. | 平均数是2.45元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
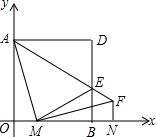 在图中,正方形AOBD的边AO,BO在坐标轴上,若它的面积为16,点M从O点以每秒1个单位长度的速度沿x轴正方向运动,当M到达B点时,运动停止.连接AM,过M作AM⊥MF,且满足AM=MF,连接AF交BD于E点,过F作FN⊥x轴于N,连接ME.设点M运动时间为t(s).
在图中,正方形AOBD的边AO,BO在坐标轴上,若它的面积为16,点M从O点以每秒1个单位长度的速度沿x轴正方向运动,当M到达B点时,运动停止.连接AM,过M作AM⊥MF,且满足AM=MF,连接AF交BD于E点,过F作FN⊥x轴于N,连接ME.设点M运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com