
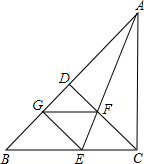
 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G,请判断四边形GECF的形状,并证明你的结论.
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G,请判断四边形GECF的形状,并证明你的结论. 分析 根据全等三角形的判定定理HL进行证明Rt△AEG≌Rt△AEC(HL),得到GE=EC;根据平行线EG∥CD的性质、∠BAC平分线的性质以及等量代换推知∠FEC=∠CFE,易证CF=CE;从而根据邻边相等的平行四边形是菱形进行判断.
解答 四边形GECF是菱形,
证明:∵∠ACB=90°,
∴AC⊥EC.
又∵EG⊥AB,AE是∠BAC的平分线,
∴GE=CE.
在Rt△AEG与Rt△AEC中,
$\left\{\begin{array}{l}{GE=CE}\\{AE=AE}\end{array}\right.$,
∴Rt△AEG≌Rt△AEC(HL);
∴GE=EC,
∵CD是AB边上的高,
∴CD⊥AB.
又∵EG⊥AB,
∴EG∥CD,
∴∠CFE=∠GEA.
∵Rt△AEG≌Rt△AEC,
∴∠GEA=∠CEA,
∴∠CEA=∠CFE,即∠CEF=∠CFE,
∴CE=CF,
∴GE=EC=FC.
又∵EG∥CD,即GE∥FC,
∴四边形GECF是菱形.
点评 本题考查了菱形的判定、全等三角形的判定与性质,关键是掌握菱形的判定:
①菱形定义:一组邻边相等的平行四边形是菱形;
②四条边都相等的四边形是菱形.
③对角线互相垂直的平行四边形是菱形.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于E,若∠EAO=15°,则∠BOE的度数为( )
如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于E,若∠EAO=15°,则∠BOE的度数为( )| A. | 85° | B. | 80° | C. | 75° | D. | 70° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
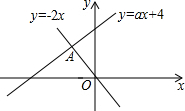 如图,函数y=-2x和y=ax+4的图象相交于A(m,3),则关于x的不等式0<ax+4<-2x的解集是-6<x<-$\frac{3}{2}$.
如图,函数y=-2x和y=ax+4的图象相交于A(m,3),则关于x的不等式0<ax+4<-2x的解集是-6<x<-$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com