
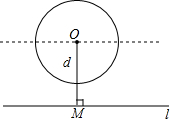 如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
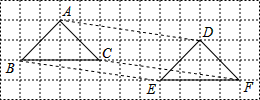 如图,△ABC平移到△DEF的位置,则下列说法:
如图,△ABC平移到△DEF的位置,则下列说法:| A. | ①② | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
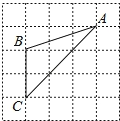 如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )| A. | $\frac{1}{3}$$\sqrt{3}$ | B. | $\frac{1}{5}$$\sqrt{5}$ | C. | $\frac{2}{5}$$\sqrt{5}$ | D. | $\frac{2}{3}$$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
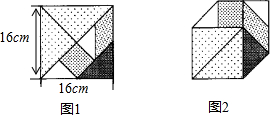 七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.
七巧板是我们祖先的一项卓越创造,被誉为“东方魔板”,小明利用七巧板(如图1所示)中各板块的边长之间的关系拼成一个凸六边形(如图2所示),则该凸六边形的周长是(32$\sqrt{2}$+16)cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
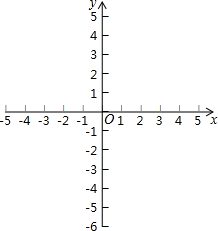 已知一次函数y=2x+4
已知一次函数y=2x+4查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1•x2<0 | B. | x1•x3<0 | C. | x2•x3<0 | D. | x1+x2<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com