
【题目】如图,在Rt△ABC中,∠C=90°,D为AC上一点,连接BD,DF⊥BD交AB于点F,△BDF的外接圆⊙O与边BC相较于点M,与AC相切于点D。过点M作AB的垂线交BD于点E,交⊙O于点N,交AB于点H,连接FN.
(1)求证:BD平分∠ABC;
(2)连接FM与BD相交于点K,求证:MK=ME;
(3)若AF=1,tan∠N=![]() ,求BE的长.
,求BE的长.
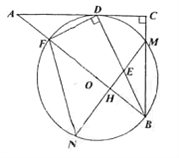
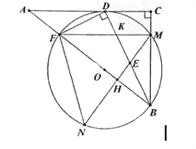
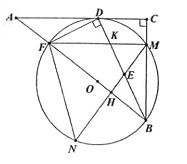
【答案】(1)证明见解析;(2)证明见解析;(3) ![]() .
.
【解析】试题分析:(1)连接OD,由OD=OB得∠ODB=∠OBD,再证明OD//BC,从而得∠ODB=∠DBC,得到∠OBD=∠DBC,问题得证;
(2)证明∠MKE=∠MEK即可得;
(3)先证得FB为⊙O的直径,根据tan∠N=tan∠ABC=![]() ,从而得tan∠BAC=
,从而得tan∠BAC=![]() ,设OD=r=3
,设OD=r=3![]() ,则有AD=4
,则有AD=4![]() ,AO=5
,AO=5![]() ,从而可求得
,从而可求得![]() =
=![]() , r=
, r=![]() ,继而得到BF=3,AB=4, BC=
,继而得到BF=3,AB=4, BC=![]() ,连接BN,从而可得BH的长,再根据∠DBC=∠DBF,得
,连接BN,从而可得BH的长,再根据∠DBC=∠DBF,得![]() ,求得BD的长,再根据
,求得BD的长,再根据![]() , 即可求得BE的长.
, 即可求得BE的长.
试题解析:(1)连接OD,∵OD=OB,∴∠ODB∠OBD,
∵AC是⊙O的切线,∴∠ODA=∠C=90 ,∴OD∥BC,∴∠ODB=∠DBC,
∴∠OBD=∠DBC,
即BD平分∠ABC;

(2)∵∠BHE=90°,∠FBD=∠DBC,
∴∠MEK=∠BEH=90-∠FBD=90-∠DBC,
又∵∠MKE=∠DKF=90 -∠DFK,∠DFK=∠DBC,
.∴∠MKE=∠MEK,∴MK=ME;
(3)∵DF⊥BD, ∴∠FDB=90 ,∴FB为⊙O的直径,
∵tan∠N=tan∠ABC=![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴tan∠BAC=![]() ,设OD=r=3
,设OD=r=3![]() ,∴AD=4
,∴AD=4![]() ,AO=5
,AO=5![]() ,
,
∴5![]() =3
=3![]() +1,∴
+1,∴![]() =
=![]() ,∴r=
,∴r=![]() ,
,
∴BF=3,AB=4, BC=![]() ,
,
连接BN,∴∠FNB=90 ,∴BN=![]() BF, BH=
BF, BH=![]() BN,
BN,
∴BH=![]() ×
×![]() ×3=
×3=![]() ,
,
∵∠DBC=∠DBF,∴ ![]() ,∴BD=
,∴BD=![]() ,
,
∴![]() , 即
, 即 , ∴BE=
, ∴BE=![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.
(1)求证:∠BAD=∠DAE;
(2)若AB=6,AD=5,求DF的长.
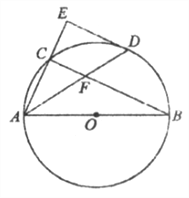
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
轴交于A(-3,0),B(1,0)两点,与y轴交于点C.

(1)求这个二次函数的解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
(3)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于![]() 轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,对称轴交BE于点F,点D,E的坐标分别为(3,0),(0,1).
(1)求抛物线的解析式;
(2)猜想△EDB的形状并加以证明;
(3)点M在对称轴右侧的抛物线上,点N在x轴上,请问是否存在以点A,F,M,N为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过平行四边形ABCD对角线交点O的线段EF,分别交AD,BC于点E,F,当AE=ED时,△AOE的面积为4,则四边形EFCD的面积是( )
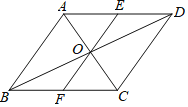
A.8B.12C.16D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
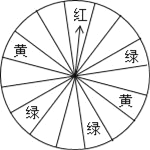
【题目】“六一”儿童节期间,某商厦为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准哪个区域,顾客就可以获得相应的奖品.
颜色 | 奖品 |
红色 | 玩具熊 |
黄色 | 童话书 |
绿色 | 彩笔 |
小明和妈妈购买了125元的商品,请你分析计算:
(1)小明获得奖品的概率是多少?
(2)小明获得童话书的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解:
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右)爬行记为“+”,向下(或向左)爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
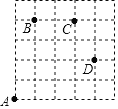
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
(1)图中B→C( , )C→D( , )
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC中,∠C=90°,AB的垂直平分线交AC于点D,连接BD. 若AC=2,BC=1,则△BCD的周长为___________________.
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中求作△EDF.(要求:尺规作图,不写作法,保留作图痕迹)
②在图3中补全图形,求∠EOF的度数.
③若![]() ,则
,则![]() =_______________.
=_______________.

图1 图2 图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com