Question

边长分别为3，4，5的三角形内切圆的面积为________．

Answer 1

π
分析：根据勾股定理的逆定理求出∠C=90°，连接OD、OF，设圆O的半径是r，G根据三角形的内切圆得到CD=CF，AE=AD，BE=BF，OD=OF，∠ODC=∠C=∠OFC=90°，证正方形ODCF得出CD=CF=OD，即可推出AC-OD+BC-OD=AB，代入求出半径即可．
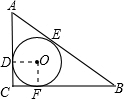
解答：解：如图，
∵AC²+BC²=3²+4²=25，
AB²=5²=25，
∴AC²+BC²=AB²，
∴∠C=90°，
连接OD、OF，
设圆O的半径是r，
∵圆O是△ABC的内切圆，切点分别是D、E、F，
∴CD=CF，AE=AD，BE=BF，OD=OF，∠ODC=∠C=∠OFC=90°，
∴四边形ODCF是正方形，
∴OD=OF=CF=CD=r，
∴AC-OD+BC-OD=AB，
3-r+4-r=5，
解得：r=1，
故它的内切圆面积为π×1²=π．
故答案为：π．
点评：本题主要考查了勾股定理的逆定理，正方形的性质和判定，切线长定理，三角形的内切圆与内心等知识点的理解和掌握，能根据这些性质推出3-r+4-r=5是解此题的关键．