
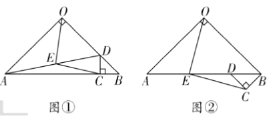
【题目】如图①,在![]() 中,
中,![]() 为
为![]() 边上一点,过
边上一点,过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(观察猜想)
(1)①![]() 的数量关系是___________
的数量关系是___________
②![]() 的数量关系是______________
的数量关系是______________
(类比探究)
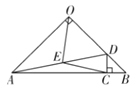
(2)将图①中![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(拓展迁移)
(3)将![]() 绕点
绕点![]() 旋转任意角度,若
旋转任意角度,若![]() ,请直接写出点
,请直接写出点![]() 在同一直线上时
在同一直线上时![]() 的长.
的长.
【答案】(1)①![]() ;②
;②![]() ;(2)成立,证明见解析;(3)
;(2)成立,证明见解析;(3)![]() 的长为
的长为![]() 或
或![]()
【解析】
(1)①根据直角三角形斜边上的中线等于斜边的一半,即可得到答案;
②由①知![]() ,利用等边对等角和三角形的外角性质,得到
,利用等边对等角和三角形的外角性质,得到![]() ,
,![]() ,然后即可得到答案;
,然后即可得到答案;
(2)①过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,EF与
,EF与![]() 交于点
交于点![]() ,利用等腰直角三角形的性质,证明
,利用等腰直角三角形的性质,证明![]() ,即可得到结论成立;
,即可得到结论成立;
②由全等三角形的性质,求出∠OEC=90°,即可得到结论成立;
(3)根据旋转的性质,点![]() 在同一直线上可分为两种情况:①点C在线段OB上;②点C在OB的延长线上;利用等腰直角三角形的性质,分别求出OE的长度,即可得到答案.
在同一直线上可分为两种情况:①点C在线段OB上;②点C在OB的延长线上;利用等腰直角三角形的性质,分别求出OE的长度,即可得到答案.
解:(1)如图,在△AOD和△ACD中,
∵![]() ,
,![]() 为AD中点,
为AD中点,
![]() ,
,
![]() ,E为AD中点,
,E为AD中点,
![]() ,
,
![]() ;
;
②![]() ,
,![]() 为AD中点,
为AD中点,
![]()
![]() ,
,
∴![]() ;
;
同理可得:![]() ,
,
![]() ,
,
![]() .
.
(2)成立.
证明:①如图,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 与
与![]() 交于点
交于点![]() ,
,
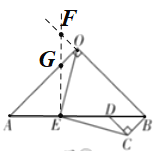
∵![]() 是等腰三角形,
是等腰三角形,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 均为等腰直角三角形,
均为等腰直角三角形,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
②![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)![]() 的长为
的长为![]() 或
或![]() ;
;
∵在等腰直角![]() 中,
中,![]() ,
,
![]() ,
,
由(2)可知,![]() ,
,![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ;
;
当点![]() 在同一直线上时,有
在同一直线上时,有
①点C在线段OB上;如图:
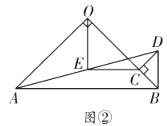
∴![]() ,
,
∴![]() ;
;
②点C在OB的延长线上;如图:

∴![]() ,
,
∴![]() ;
;
综上所述,![]() 的长为
的长为![]() 或
或![]() ;
;


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校组织七年级学生参加冬令营活动,本次冬令营活动分为甲、乙、丙三组进行.如图,条形统计图和扇形统计图反映了学生参加冬令营活动的报名情况,请你根据图中的信息回答下列问题:
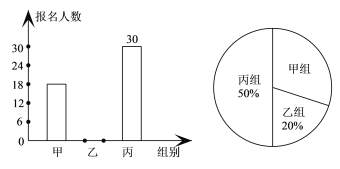
(1)七年级报名参加本次活动的总人数为 ,扇形统计图中,表示甲组部分的扇形的圆心角是 度;
(2)补全条形统计图;
(3)根据实际需要,将从甲组抽调部分学生到丙组,使丙组人数是甲组人数的3倍,则应从甲组抽调多少名学生到丙组?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场的运动服装专柜,对![]() 两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
第一次 | 第二次 | |
| 20 | 30 |
| 30 | 40 |
累计采购款/元 | 10200 | 14400 |
(1)问![]() 两种品牌运动服的进货单价各是多少元?
两种品牌运动服的进货单价各是多少元?
(2)由于![]() 品牌运动服的销量明显好于
品牌运动服的销量明显好于![]() 品牌,商家决定采购
品牌,商家决定采购![]() 品牌的件数比
品牌的件数比![]() 品牌件数的
品牌件数的![]() 倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件
倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件![]() 品牌运动服?
品牌运动服?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线![]() 平行于直线EC,且直线
平行于直线EC,且直线![]() 与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线
与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线![]() 上, 则DF的长为_____
上, 则DF的长为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
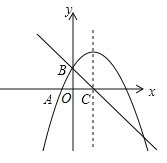
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() ,图像的对称轴交
,图像的对称轴交![]() 轴于点
轴于点![]() ,一次函数
,一次函数![]() 的图像经过点
的图像经过点![]() .
.
(1)求二次函数的解析式![]() 和一次函数的解析式
和一次函数的解析式![]() ;
;
(2)点![]() 在
在![]() 轴下方的二次函数图像上,且
轴下方的二次函数图像上,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)结合图像,求当![]() 取什么范围的值时,有
取什么范围的值时,有![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,斜坡AB的长为65米,坡度i=1∶2.4,BC⊥AC.
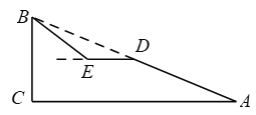
(参考三角函数:sin37°≈ ![]() ,cos37°≈
,cos37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() )
)
(1)求斜坡的高度BC.
(2)现计划在斜坡AB的中点D处挖去部分坡体,修建一个平行于水平线CA的平台DE和一条新的斜坡BE,若斜坡BE的坡角为37°,求平台DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:6cos45°+(![]() ﹣1.73)0+|5﹣3
﹣1.73)0+|5﹣3![]() |+42017×(﹣0.25)2017;
|+42017×(﹣0.25)2017;
(2)先化简,再求值:(![]() ﹣a+1)÷
﹣a+1)÷![]() ﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,AB=AC,∠A=40O,延长AC到D,使CD=BC,点P是ΔABD的内心,则∠BPC=

A. 105° B. 110° C. 130° D. 145°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com