Question

7．为了了解某校九年级学生数学质量检测成绩情况，检测教师随机抽取该校九年级上学期期末数学考试部分学生成绩（得分为整数，满分为150分）分为5组：第一组75～90；第二组90～105；第三组105～120；第四组120～135；第五组135～150．统计后得到如图所示的频数分布直方图（每组含最小值不含最大值）和扇形统计图．观察图形的信息，回答下列问题：
（1）本次调查共随机抽取了该年级多少名学生？并将频数分布直方图补充完整：
（2）若将得分转化为等级，规定：得分低于90分评为“D”，90～120分评为“C”，120～135分评为“B”，135～150分评为“A”，那么该校九年级450名考生中，考试成绩评为“C”的学生大约有多少名？
（3）如果第一组有两名女生，第五组只有一名男生，检测教师决定从第一组、第五组分别随机选出一名同学谈谈做题的感想，用列表或画树状图的方法求出所选两名学生刚好是一名女生和一名男生的概率．

Answer 1

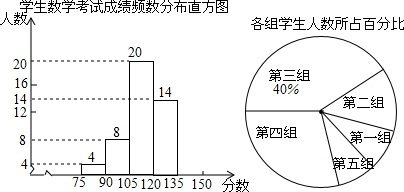
分析 （1）根据第三组的人数以及百分比，求得本次调查共随机抽取的学生数，再用总人数减去前4组的人数，可得第五组的人数；
（2）根据考试成绩评为“C”的学生数占抽取的学生数的百分比，乘上该校九年级考生数，求得该校九年级考生中考试成绩评为“C”的学生数；
（3）先根据题意画出树状图，根据所得结果中所选两名学生刚好是一名女生和一名男生的结果数，求得概率．

解答 解：（1）根据题意得，本次调查共随机抽取的学生数为：20÷40%=50（名），
∴第五组的人数为：50-4-8-20-14=4（名），频数分布直方图如下；

（2）根据题意得，该校九年级450名考生中，考试成绩评为“C”的学生大约有：$\frac{28}{50}$×450=252（名）；
（3）画树状图得：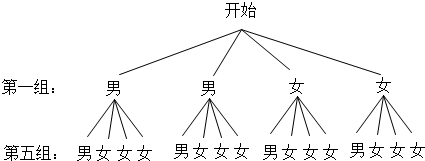

∵16种结果中，所选两名学生刚好是一名女生和一名男生的结果有8种，
∴所选两名学生刚好是一名女生和一名男生的概率为：$\frac{8}{16}$=$\frac{1}{2}$．

点评 本题主要考查了运用画树状图计算概率，当有两个元素时，可用树形图列举，也可以列表列举．一般来说，用样本去估计总体时，样本越具有代表性、容量越大，这时对总体的估计也就越精确．