
【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送![]() 批客人,行驶路程记录如下(规定向东为正,向西为负,单位:
批客人,行驶路程记录如下(规定向东为正,向西为负,单位:![]() ):
):
第 | 第 | 第 | 第 | 第 |
|
|
|
|
|
(1)接送完第![]() 批客人后,该驾驶员在公司什么方向,距离公司多少千米?
批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油![]() 升,那么在这过程中共耗油多少升?
升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过![]() 收费
收费![]() 元,超过
元,超过![]() 的部分按每千米
的部分按每千米![]() 元收费,在这过程中该驾驶员共收到车费多少元?
元收费,在这过程中该驾驶员共收到车费多少元?
【答案】(1)在公司的东边10千米处;(2)共耗油4.8升;(3)共收到车费68元.
【解析】
(1)由题意把接送![]() 批客人的行驶路程相加,并进行计算即可;
批客人的行驶路程相加,并进行计算即可;
(2)根据题意先计算出总行驶路程,再乘以出租车每千米耗油![]() 升即可求出在这过程中共耗油多少升;
升即可求出在这过程中共耗油多少升;
(3)根据题意分别计算出各个批次所收到的车费,再进行相加即可.
解:(1)5+2+(-4)+(-3)+10=10(km).
由题意可知规定向东为正,向西为负,
答:接送完第5批客人后,该驾驶员在公司的东边10千米处.
(2)由题意出租车每千米耗油![]() 升可得:
升可得:
(5+2+|-4|+|-3|+10)×0.2=24×0.2=4.8(升).
答:在这个过程中共耗油4.8升.
(3)[10+(5-3)×1.8]+10+[10+(4-3)×1.8]+10+[10+(10-3)×1.8]=68(元).
答:在这个过程中该驾驶员共收到车费68元.


科目:初中数学 来源: 题型:
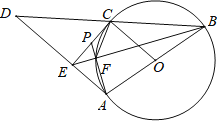
【题目】如图,AB为圆O的直径,C为圆O上一点,D为BC延长线一点,且BC=CD,CE⊥AD于点E.
(1)求证:直线EC为圆O的切线;
(2)设BE与圆O交于点F,AF的延长线与CE交于点P,已知∠PCF=∠CBF,PC=5,PF=4,求sin∠PEF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于![]() BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
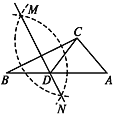
A. 90°B. 95°C. 100°D. 105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,其中
,其中![]() .
.
(1)若点![]() 在y1的图象上.求a的值:
在y1的图象上.求a的值:
(2)当![]() 时.若函数有最大值2.求y1的函数表达式;
时.若函数有最大值2.求y1的函数表达式;
(3)对于一次函数![]() ,其中
,其中![]() ,若对- -切实数x,
,若对- -切实数x,![]() 都成立,求a,m需满足的数量关系及 a的取值范围.
都成立,求a,m需满足的数量关系及 a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
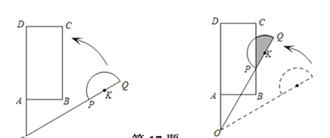
【题目】平面上,矩形ABCD与直径为QP的半圆K如图如图①摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针开始旋转,如图②,当点P恰好落在BC边上时,S阴影=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
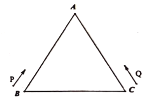
【题目】如图,等边三角形![]() 的周长为
的周长为![]() ,
,![]() ,
,![]() 两点分别从
两点分别从![]() ,
,![]() 两点同时出发,点
两点同时出发,点![]() 以
以![]() 的速度按顺时针方向在三角形的边上运动,点
的速度按顺时针方向在三角形的边上运动,点![]() 以
以![]() 的速度按逆时针方向在三角形的边上运动.设
的速度按逆时针方向在三角形的边上运动.设![]() ,
,![]() 两点第一次在三角形
两点第一次在三角形![]() 的顶点处相遇的时间为
的顶点处相遇的时间为![]() ,第二次在三角形
,第二次在三角形![]() 顶点处相遇的时间为
顶点处相遇的时间为![]() ,则
,则![]() _______.
_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 和点
和点![]() 在数轴上对应的数分别为
在数轴上对应的数分别为![]() 和
和![]() ,且
,且![]() .
.
(1)线段![]() 的长为 ;
的长为 ;
(2)点![]() 在数轴上所对应的数为
在数轴上所对应的数为![]() ,且
,且![]() 是方程
是方程![]() 的解,在线段
的解,在线段![]() 上是否存在点
上是否存在点![]() 使得
使得![]() ?若存在,请求出点
?若存在,请求出点![]() 在数轴上所对应的数,若不存在,请说明理由;
在数轴上所对应的数,若不存在,请说明理由;
(3)在(2)的条件下,线段![]() 和
和![]() 分别以6个单位长度/秒和5个单位长度/秒的速度同时向右运动,运动时间为
分别以6个单位长度/秒和5个单位长度/秒的速度同时向右运动,运动时间为![]() 秒,点
秒,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点,若
的中点,若![]() ,求
,求![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的几个式子:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;…
;…
(1)根据上面的规律,第5个式子为:________________.
(2)根据上面的规律,第n个式子为:________________.
(3)利用你发现的规律,写出![]() …
…![]() ________________.
________________.
(4)利用你发现的规律,求出![]() …
…![]() 的值,并写出过程。
的值,并写出过程。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com