
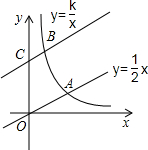
 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移3个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,若OA=3BC,则k的值为$\frac{81}{32}$.
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移3个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,若OA=3BC,则k的值为$\frac{81}{32}$. 分析 作AE⊥y轴于E,BF⊥y轴于F.由△AEO∽△BFC,得到=$\frac{BF}{AE}$=$\frac{BC}{OA}$=$\frac{1}{3}$,设A(m,$\frac{1}{2}$m),则B($\frac{1}{3}$m,$\frac{1}{6}$m+3),想办法列方程组求出m、k即可.
解答 解:如图,作AE⊥y轴于E,BF⊥y轴于F.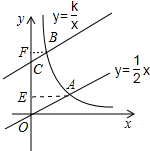
∵OA∥BC,
∴∠BCF=∠AOE,∵∠BFC=∠AEO,
∴△AEO∽△BFC,
∴$\frac{BF}{AE}$=$\frac{BC}{OA}$=$\frac{1}{3}$,设A(m,$\frac{1}{2}$m),则B($\frac{1}{3}$m,$\frac{1}{6}$m+3),
由题意$\left\{\begin{array}{l}{\frac{1}{6}m+3=\frac{3k}{m}}\\{\frac{1}{2}{m}^{2}=k}\end{array}\right.$解得$\left\{\begin{array}{l}{m=\frac{9}{4}}\\{k=\frac{81}{32}}\end{array}\right.$,
∴K=$\frac{81}{32}$,
故答案为$\frac{81}{32}$.
点评 本题考查一次函数与反比例函数的交点问题、相似三角形的判定和性质,二元一次方程组等知识,解题的关键是学会添加常用辅助线构造相似三角形,学会利用方程组解决问题,属于中考常考题型.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:选择题
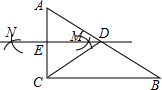 如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于$\frac{1}{2}$AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A和点C为圆心,以相同的长(大于$\frac{1}{2}$AC)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.下列结论错误的是( )| A. | AD=CD | B. | ∠A=∠DCE | C. | ∠ADE=∠DCB | D. | ∠A=2∠DCB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠C为直角,CD⊥AB于D,已知AC=3,AB=5,则tan∠BCD等于( )
如图,在Rt△ABC中,∠C为直角,CD⊥AB于D,已知AC=3,AB=5,则tan∠BCD等于( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
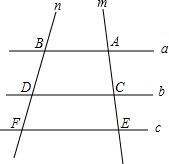 如图,已知a∥b∥c,n,m分别与a,b,c交于点B,D,F和点A,C,E,试解决下列问题:
如图,已知a∥b∥c,n,m分别与a,b,c交于点B,D,F和点A,C,E,试解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1$\frac{1}{2}$ab2 | B. | -$\frac{ab}{2}$ | C. | x+3千米 | D. | ab•3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com