
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.

(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
【答案】(1)见解析;
(2)四边形ADCF是正方形.
【解析】
试题分析:(1)由E是AD的中点,AF∥BC,易证得△AEF≌△DEB,即可得AD=BD,又由在△ABC中,∠BAC=90°,AD是中线,根据直角三角形斜边的中线等于斜边的一半,即可证得AD=BD=CD=![]() BC,即可证得:AD=AF;
BC,即可证得:AD=AF;
(2)由AF=BD=DC,AF∥BC,可证得:四边形ADCF是平行四边形,又由AB=AC,根据三线合一的性质,可得AD⊥BC,AD=DC,继而可得四边形ADCF是正方形.
试题解析:(1)∵AF∥BC,
∴∠EAF=∠EDB,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,
∠EAF=∠EDB,AE=DE,∠AEF=∠DEB,
∴△AEF≌△DEB(ASA),
∴AF=BD,
∵在△ABC中,∠BAC=90°,AD是中线,
∴AD=BD=DC=![]() BC,
BC,
∴AD=AF;
(2)四边形ADCF是正方形.
∵AF=BD=DC,AF∥BC,
∴四边形ADCF是平行四边形,
∵AB=AC,AD是中线,
∴AD⊥BC,
∵AD=AF,
∴四边形ADCF是正方形.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】数学兴趣小组成员张广益对本年级期中考试数学成绩(成绩取整数,满分为100分)做了统计分析,绘制成如下频数、频率分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题:
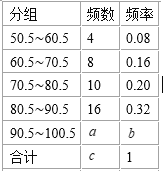
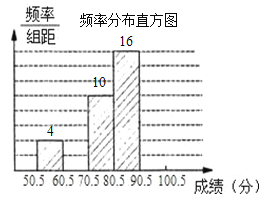
⑴填充频率分布表中的空格:a ,b ,c ;
⑵补全频率分布直方图;
⑶已知本年级共计1700名学生,若竞赛成绩在90分以上(不含90分)为优秀,估算本年级数学成绩优秀的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知A(-4,-1),B(-5,-4),C(-1,-3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请在图中作出△A′B′C′;(2)写出点A′、B′、C′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 一次函数y=﹣2x+3,y随x的增大而减小,
B. 反比例函数![]() 中,y随x的增大而增大,
中,y随x的增大而增大,
C. 抛物线y=x2+1与y=x2﹣1的形状相同,只是位置不同,
D. 二次函数y=﹣2(x﹣2)2+3中,当x>2时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,AB=AC,点D、点O分别为BC、AC的中点,AE//BC.
(1)如图1,求证:四边形ADCE是矩形;
(2)如图2,若点 F是 CE上一动点,在不添加任何辅助线的情况下,请直接写出与四边形 ABDF 面积相等的三角形和四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在四边形ABCD中,AD∥BC,AB∥DC,点E在BC延长线上,连接DE,∠A+∠E=180°.
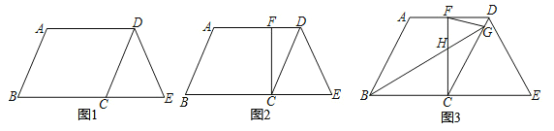
(1)如图1,求证:CD=DE;
(2)如图2,过点C作BE的垂线,交AD于点F,请直接写出BE、AF、DF 之间的数量关系_______________________;
(3)如图3,在(2)的条件下,∠ABC的平分线,交CD于G,交CF于H,连接FG,若∠FGH=45°,DF=8,CH=9,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图1,图2所提供的信息,解答下列问题:
(1)2007年海南省城镇居民人均可支配收入为 元,比2006年增长 %;
(2)求2008年海南省城镇居民人均可支配收入(精确到1元),并补全条形统计图;
(3)根据图1指出:2005﹣2008年海南省城镇居民人均可支配收入逐年 (填“增加”或“减少”).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com