
 已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm,点P从点B出发,沿BA方向匀速运动,速度为1cm/s,同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm,点P从点B出发,沿BA方向匀速运动,速度为1cm/s,同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:分析 (1)当AP=DF时,四边形APFD为平行四边形,用t表示出AP=10-t,DF=$\frac{5}{4}$t,列等式计算;
(2)作高CM,利用面积相等求出CM的长,由图可知:四边形APFE的面积=四边形APFD的面积-△EFD的面积;代入求出y与t之间的函数关系式,再求二次函数的顶点坐标的横坐标即可;
(3)先计算菱形ABCD的面积,再将(2)得到的y代入到式子S四边形APFE:S菱形ABCD=17:40中,解出即可.
解答 解:(1)∵四边形ABCD为菱形,
∴BO=$\frac{1}{2}$BD=$\frac{1}{2}$×16=8,AO=$\frac{1}{2}$AC=$\frac{1}{2}$×12=6,AC⊥BD,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
由题意可知:BP=t,DQ=t,则AP=10-t,
∵FQ∥OC,
∴$\frac{FQ}{OC}=\frac{DQ}{OD}$,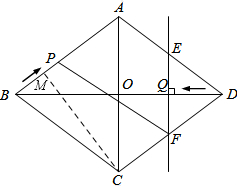
∴$\frac{FQ}{6}=\frac{t}{8}$,
∴FQ=$\frac{3}{4}$t,
∵EF⊥BD,
由勾股定理得:DF=$\sqrt{{t}^{2}+(\frac{3}{4}t)^{2}}$=$\frac{5}{4}$t,
∵AB∥CD,
∴AP∥DF,
∴当AP=DF时,四边形APFD为平行四边形,
则10-t=$\frac{5}{4}$t,
t=$\frac{40}{9}$;
∴当t=$\frac{40}{9}$时,四边形APFD是平行四边形;
(2)过C作CM⊥AB于M,
则S△ABC=$\frac{1}{2}$AC•BO=$\frac{1}{2}$AB•CM,
∴AC•BO=AB•CM,
∴12×8=10CM,
∴DM=9.6,
则y=S四边形APFD-S△EFD=$\frac{1}{2}$×9.6×[(10-t)+$\frac{5}{4}$t]-$\frac{1}{2}$×$\frac{3}{4}$t×2×t=-$\frac{3}{4}$t2+1.2t+48,
当t=-$\frac{1.2}{2×(-\frac{3}{4})}$=0.8时,y有最大值;
(3)存在,
S菱形ABCD=$\frac{1}{2}$×AC×BD=$\frac{1}{2}$×12×16=96,
∵S四边形APFE:S菱形ABCD=17:40,
则$\frac{-\frac{3}{4}{t}^{2}+1.2t+48}{96}=\frac{17}{40}$,
5t2-8t-48=0,
解得:t1=4,t2=-$\frac{12}{5}$(舍去),
∵0<t<8,
∴t=4符合题意,
∴当t=4时,S四边形APFE:S菱形ABCD=17:40.
点评 本题是四边形的综合题,综合考查了菱形、平行四边形的性质,本题有一动点和一动直线,此类题的解题思路为:根据速度和时间表示出路程,并依次将各条线段表示出来;再根据所成特殊四边形的性质列等式计算;本题与函数相结合,利用面积公式求函数关系式,并利用顶点坐标公式求最值.


科目:初中数学 来源: 题型:选择题
| A. | AB∥CD,AD=BC | B. | AB=CD,AD=BC | C. | ∠A=∠B,∠C=∠D | D. | AB=AD,CB=CD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
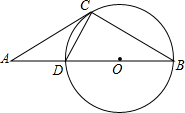 如图,点A是⊙O直径BD延长线上的一点,C在⊙O上,AC=BC,AD=CD
如图,点A是⊙O直径BD延长线上的一点,C在⊙O上,AC=BC,AD=CD查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com