

���� ��1����D���뼴�����a�������ɶ���ʽֱ��д����
��2������������C1��������C2��������ϵ����Ϊ�෴�����������ԭ��ԳƼ��ɽ����
��3��Q��E��������������ɨ�������ת��Ϊƽ���ı���EQMK�������
��� �⣺��1����������${C_1}��y=a{��{x+2}��^2}-3$��������D��0��-1��
��-1=4a-3��
��a=$\frac{1}{2}$
�ඥ��ΪP��-2��-3����
��2���������֪������C2Ϊ��y=-$\frac{1}{2}$��x-2��2+3��
��������C2�Ľ���ʽΪ��y=-$\frac{1}{2}$x2+2x+1��
��3����ͼ�����⣺Q��2��3����B��2��0��
��QB��x��
��ƽ�ƿ�֪��QB=MN=3��
��y=-3ʱ��-3=-$\frac{1}{2}$x+1��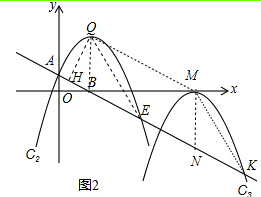
��x=8��
��������C3����M��8��0����
��������C3W��y=-$\frac{1}{2}$��x-8��2��
��QH��AB����ΪH����ֱ��QHΪ��y=2X+b��Q��2��3������õ�b=-1��
��ֱ��QHΪy=2x-1��
��$\left\{\begin{array}{l}{y=2x-1}\\{y=-\frac{1}{2}x+1}\end{array}\right.$��$\left\{\begin{array}{l}{x=\frac{4}{5}}\\{y=\frac{3}{5}}\end{array}\right.$�����Ե�H���꣨$\frac{4}{5}$��$\frac{3}{5}$����
��QH=$\sqrt{��2-\frac{4}{5}��^{2}+��3-\frac{3}{5}��^{2}}$=$\frac{6\sqrt{5}}{5}$��QM=$\sqrt{��8-2��^{2}+{3}^{2}}$=3$\sqrt{5}$
��Q��E��������������ɨ�����������ƽ���ı���QEKM�����=QM•QH=$\frac{6\sqrt{5}}{5}$$•3\sqrt{5}$=18��
���� ���⿼����κ������й�֪ʶ��������ƽ�Ƶ����ʡ�һ�κ��������ʡ�ƽ���ı��ε������֪ʶ�����������߹���ԭ��ԳƵ������ǽ������Ĺؼ���


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д� �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m=n | B�� | m��n | C�� | m��n | D�� | ���ж� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��A��BΪ��·lͬ�Ե�������ׯ����l����һ��P��
��ͼ��ʾ��A��BΪ��·lͬ�Ե�������ׯ����l����һ��P���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AC=AE��AB=AD��BC��DE�ཻ��F����1=��2=25�㣮
��ͼ��AC=AE��AB=AD��BC��DE�ཻ��F����1=��2=25�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com