
(12分)如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0),B(4,0),C(0,2)三点
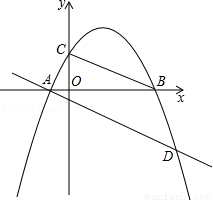
(1)求这条抛物线的解析式;
(2)E为抛物线上一动点,是否存在点E使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由;
(1)y=-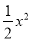 +
+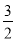 x+2;(2)E点坐标为(0,2),(3,2).
x+2;(2)E点坐标为(0,2),(3,2).
【解析】
试题分析:(1)首先设出函数的解析式,然后利用待定系数法进行求解;(2)首先根据题意判定△ABE只能是以点E为直角顶点的三角形,然后求出BC的长度,根据三角形相似求出点E的坐标.
试题解析:(1)∵抛物线经过点C(0,2) ∴设该抛物线的解析式为y=a +bx+2
+bx+2
将A、B两点坐标代入解析式得: 解得:
解得:
∴抛物线的解析式为:y=-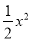 +
+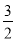 x+2
x+2
(2)存在
由图象可知,以A、B为直角顶点的△ABE不存在,所以△ABE只可能
是以点E为直角顶点的三角形.

在Rt△BOC中,OC=2,OB=4, ∴BC= =
=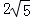 .
.
在Rt△BOC中,设BC边上的高为h,则 ×
×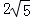 h=
h= ×2×4, ∴h=
×2×4, ∴h=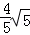 .
.
∵△BEA∽△COB,设E点坐标为(x,y), ∴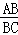 =
= ,∴y=±2
,∴y=±2
将y=2代入抛物线y=-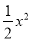 +
+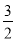 x+2,得
x+2,得 =0,
=0,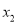 =3.
=3.
当y=﹣2时,不合题意舍去.
∴E点坐标为(0,2),(3,2).
考点:待定系数法求函数解析式、三角形相似的应用.
考点分析: 考点1:二次函数 定义: (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。  (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性


科目:初中数学 来源:2014-2015学年山东省枣庄市九年级3月测试数学试卷(解析版) 题型:填空题
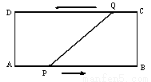
如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P,Q分别从A,C,同时出发,点P以2cm/s的速度向点B移动,到达B点后停止,点Q以1cm/s的速度向点D移动,到达D点后停止,P,Q两点出发后,经过_____________秒时,线段PQ的长是10cm.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级学业水平考试模拟考数学试卷(解析版) 题型:选择题
有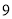 名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前
名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前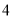 名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这
名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这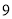 名同学成绩的( ).
名同学成绩的( ).
A.众数 B.中位数 C.平均数 D.方差
查看答案和解析>>
科目:初中数学 来源:2014-2015学年辽宁省东港市九年级九校联考数学试卷(解析版) 题型:解答题
(12分)某联欢会上有一个有奖游戏,规则如下:有5张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,其余3张是哭脸.现将5张纸牌洗匀后背面朝上摆放到桌上,若翻到的纸牌中有笑脸就有奖,没有笑脸就没有奖.
(1)小芳获得一次翻牌机会,她从中随机翻开一张纸牌.小芳得奖的概率是 .
(2)小明获得两次翻牌机会,他同时翻开两张纸牌.小明认为这样得奖的概率是小芳的两倍,你赞同他的观点吗?请用树形图或列表法进行分析说明.(用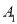 、
、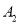 分别代表两张笑脸,
分别代表两张笑脸,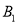 、
、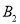 、
、 分别代表三张哭脸)
分别代表三张哭脸)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com