
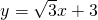 分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
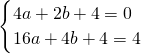 ,
,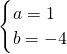 ,
,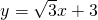 分别交x轴、y轴于B、A两点,
分别交x轴、y轴于B、A两点, ,0).
,0). .
. 时,BG=2+
时,BG=2+ ,AG=2+
,AG=2+ ,
, ,
, 时,BG=2-
时,BG=2- ,AG=2-
,AG=2- ,
, ,3).
,3). ,
, +n.
+n.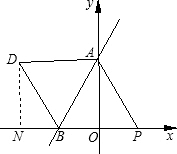
 +n,∠DBN=60°,
+n,∠DBN=60°, (
( +n),BN=
+n),BN=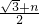 ,
, -
-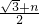 ,
,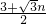 ),
),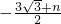 ,
,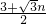 ),
),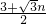 =(-
=(-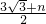 -n)2,
-n)2, +21=0.
+21=0. ,n=-
,n=-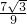 ,当n=-
,当n=- 时,P与B重合,不能构成三角形,舍去,
时,P与B重合,不能构成三角形,舍去,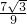 时,此时抛物线为y=(x+
时,此时抛物线为y=(x+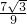 )2.
)2.

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
 曲线y=
曲线y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线l分别交x轴、y轴于A、B两点,且A(3
如图,直线l分别交x轴、y轴于A、B两点,且A(3| 3 |
| 3 |
3
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源:2010-2011学年北京市顺义区李桥中学九年级(上)第三次月考数学试卷(解析版) 题型:解答题
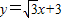 分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
分别交x轴、y轴于B、A两点,抛物线L:y=ax2+bx+c的顶点G在x轴上,且过(0,4)和(4,4)两点.
查看答案和解析>>
科目:初中数学 来源:2006年湖北省咸宁市中考数学试卷(解析版) 题型:解答题
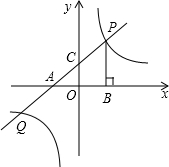
 x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y=
x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y= 在第一象限内的交点,PB⊥x轴,垂足为点B,△APB的面积为4.
在第一象限内的交点,PB⊥x轴,垂足为点B,△APB的面积为4.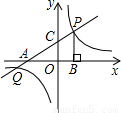
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com