
【题目】如图,∠AOB是平角,OD是∠AOC的角平分线,∠COE=∠BOE.
(1)若∠AOC= 50°,则∠DOE= °;
(2)若∠AOC= 50°,则图中与∠COD互补的角为 ;
(3)当∠AOC的大小发生改变时,∠DOE的大小是否发生改变?为什么?

【答案】(1)90°;(2)∠BOD;(3)不发生改变,理由详见解析.
【解析】
(1)由∠AOC=50°,得到∠AOD=∠COD=25°,∠BOC=130°,求得∠COE=∠BOE=115°.即可求出∠DOE;
(2)由(1)得∠AOD=∠COD=25°,则∠BOD=155°,即可得到答案;
(3)设∠AOC=2x,则∠AOD =∠COD = x,得到∠COE=90°+x,即可得到∠DOE=90°.
解:(1)∵∠AOC=50°,
∴∠BOC=180°![]() 130°,
130°,
∵OD是∠AOC的角平分线,
∴∠AOD=∠COD=25°,
∴∠COE=∠BOE=![]() ,
,
∴∠DOE=115°![]() ;
;
故答案为:90.
(2) 由(1)知∠AOD=∠COD=25°,
∴∠BOD=155°,
∴图中与∠COD互补的角为∠BOD;
故答案为:∠BOD.
(3)不发生改变,
设∠AOC=2x .
∵OD是∠AOC的平分线,
∴∠AOD =∠COD=x,
∴∠BOC=180° 2x,
∵∠COE=∠BOE,
∴∠COE=![]() =90°+x,
=90°+x,
∴∠DOE=90°+x x=90°.


科目:初中数学 来源: 题型:
【题目】从以下四张图片中随机抽取一张,概率为 ![]() 的事件是( )
的事件是( )

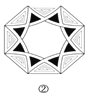


A. 是轴对称图形 B. 是中心对称图形
C. 既是轴对称图形又是中心对称图形 D. 是轴对称图形但不是中心对称图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠ACB=90°,D是边AB的中点,BE⊥CD,垂足为点E.已知AC=15,cosA=![]() .
.
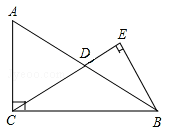
(1)求线段CD的长;
(2)求sin∠DBE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,数轴上表示1、![]() 的对应点分别为A、B,点C在OA上,且AC=AB,试求点C所表示的实数.
的对应点分别为A、B,点C在OA上,且AC=AB,试求点C所表示的实数.

(2)如图2,数轴的正半轴上有A、B、C三点,表示1和![]() 的对应点分别为A、B,点B到点A的距离与点C到点O的距离相等,设点C所表示的数为x.求(x﹣
的对应点分别为A、B,点B到点A的距离与点C到点O的距离相等,设点C所表示的数为x.求(x﹣![]() )2的立方根.
)2的立方根.
(3)如图3,a,b,c是数轴上三个点A、B、C所对应的实数.(|c|>|b|>|a|),试化简:![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明和爸爸在400米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:

(1)他们的对话内容,求小明和爸爸的骑行速度,
(2)一次追上小明后,在第二次相遇前,再经过多少分钟,小明和爸爸相距50m?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电信公司有甲、乙两种手机收费业务,仅上网流量收费不同,图中I1、I2分别表示甲、乙两种业务每月流量费用y(元)与上网流量xGB的之间的函数关系。

(1)分别求出甲、乙两种业务每月所收费用y元与上网流量xGB之间的函数关系式。
(2)已知刘老师选择了甲业务,魏老师选择了乙业务,上月两位老师所用流量相同,均为mGB,上网流量费用相差不到20元,求m的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,AC=3,∠ABC=30°.
(1)尺规作图:求作△ABC的外接圆,保留作图痕迹,不写作法;
(2)求(1)中所求作的圆的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,能判定四边形ABCD为平行四边形的个数是( )
①AB∥CD,AD=BC ; ②AB=CD,AD=BC;③∠A=∠B,∠C=∠D; ④AB=AD,CB=CD.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为_____.
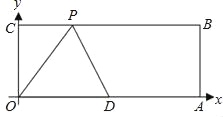
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com