练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．数据6，5，7.5，8.6，7，6的众数是（　　）
    A．5B．6C．7D．8

    分析 直接利用众数的定义分析得出答案．

    解答 解：∵数据6，5，7.5，8.6，7，6中，6出现次数最多，
    故6是这组数据的众数．
    故选：B．

    点评 此题主要考查了众数的定义，正确把握定义是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    17．已知正比例函数y=3x，若该正比例函数经过点（m，6m-1），则m的值为（　　）
    A．$\frac{1}{3}$B．-$\frac{1}{3}$C．3D．$\frac{1}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

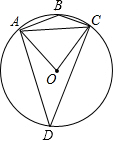    18．如图，⊙O是四边形ABCD的外接圆，连接AC，OA，OC，若∠ABC：∠ACO=13：4，则∠ADC的度数为（　　）
    A．30°B．50°C．40°D．45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

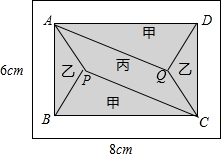    15．小黄准备给长8m，宽6m的长方形客厅铺设瓷砖，现将其划分成一个长方形ABCD区域Ⅰ（阴影部分）和一个环形区域Ⅱ（空白部分），其中区域Ⅰ用甲、乙、丙三种瓷砖铺设，且满足PQ∥AD，如图所示．
    （1）若区域Ⅰ的三种瓷砖均价为300元/m2，面积为S（m2），区域Ⅱ的瓷砖均价为200元/m2，且两区域的瓷砖总价为不超过12000元，求S的最大值；
    （2）若区域Ⅰ满足AB：BC=2：3，区域Ⅱ四周宽度相等
    ①求AB，BC的长；
    ②若甲、丙两瓷砖单价之和为300元/m2，乙、丙瓷砖单价之比为5：3，且区域Ⅰ的三种瓷砖总价为4800元，求丙瓷砖单价的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图1所示，在△ABC中，点O是AC上一点，过点O的直线与AB，BC的延长线分别相交于点M，N．
    【问题引入】
    （1）若点O是AC的中点，$\frac{AM}{BM}$=$\frac{1}{3}$，求$\frac{CN}{BN}$的值；
    温馨提示：过点A作MN的平行线交BN的延长线于点G．
    【探索研究】
    （2）若点O是AC上任意一点（不与A，C重合），求证：$\frac{AM}{MB}$•$\frac{BN}{NC}$•$\frac{CO}{OA}$=1；
    【拓展应用】
    （3）如图2所示，点P是△ABC内任意一点，射线AP，BP，CP分别交BC，AC，AB于点D，E，F，若$\frac{AF}{BF}$=$\frac{1}{3}$，$\frac{BD}{CD}$=$\frac{1}{2}$，求$\frac{AE}{CE}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．如图，四边形ABCD是菱形，⊙O经过点A、C、D，与BC相交于点E，连接AC、AE．若∠D=78°，则∠EAC=27°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

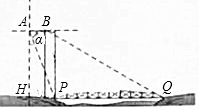    19．如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的
    俯角为α其中tanα=2$\sqrt{3}$，无人机的飞行高度AH为500$\sqrt{3}$米，桥的长度为1255米．
    ①求点H到桥左端点P的距离；  
    ②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°，求这架无人机的长度AB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．抛物线y=3x2-3向右平移3个单位长度，得到新抛物线的表达式为（　　）
    A．y=3（x-3）2-3B．y=3x2C．y=3（x+3）2-3D．y=3x2-6

    查看答案和解析>>

    科目：初中数学 来源：2017届江苏省启东市九年级寒假作业测试（开学考试）数学试卷（解析版） 题型：单选题

    如图，点D（0，3），O（0，0），C（4，0）在⊙A上，BD是⊙A的一条弦，则sin∠OBD=（　　）

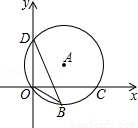
    A. B. C. D.

    查看答案和解析>>

    同步练习册答案