练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

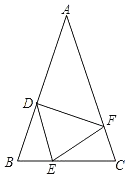
    【题目】如图，在△ABC中，AB＝AC，∠A＝48°，点D、E、F分别在BC、AB、AC边上，且BE＝CF，BD＝CE，求∠EDF的度数．

    【答案】57°

    【解析】

    根据△BDE≌△CEF，可知∠FEC＝∠BDE，∠DEF＝180°﹣∠BED﹣∠FEC＝180°﹣∠DEB﹣∠EDB＝∠B即可得出结论，再根据等腰三角形的性质即可得出∠DEF的度数．

    解：∵AB＝AC，∠A＝48°，

    ∴∠B＝∠C＝（180°﹣48°）÷2＝66°．

    在△DBE和△ECF中，

    ，

    ∴△DBE≌△ECF（SAS）．

    ∴∠FEC＝∠BDE，

    ∴∠DEF＝180°﹣∠BED﹣∠FEC

    ＝180°﹣∠DEB﹣∠EDB＝∠B＝66°．

    ∵△DBE≌△ECF（SAS），

    ∴DE＝FE．

    ∴△DEF是等腰三角形．

    ∴∠EDF＝（180°﹣66°）÷2＝57°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

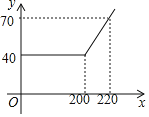
    【题目】某网络公司推出了一系列上网包月业务，其中的一项业务是10M“40元包200小时”，且其中每月收取费用y（元）与上网时间x（小时）的函数关系如图所示．

    （1）当x≥200时，求y与x之间的函数关系式

    （2）若小刚家10月份上网180小时，则他家应付多少元上网费？

    （3）若小明家10月份上网费用为52元，则他家该月的上网时间是多少小时？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB＝90°，∠ABC＝30°，△CDE是等边三角形，点D在边AB上．

    （1）如图1，当点E在边BC上时，求证DE＝EB；

    （2）如图2，当点E在△ABC内部时，猜想ED和EB数量关系，并加以证明；

    （3）如图3，当点E在△ABC外部时，EH⊥AB于点H，过点E作GE∥AB，交线段AC的延长线于点G，AG＝5CG，BH＝3．求CG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC 中，AB=AC，CD是∠ACB的平分线，DE∥BC，交AC于点 E．

    （1）求证：DE=CE．

    （2）若∠CDE=35°，求∠A 的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD是∠BAC的平分线．若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是（ ）

    A. B. 4 C. D. 5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，，AD是的中线，AE是的角平分线，交AE的延长线于点F，则DF的长为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知和都是等腰直角三角形，点D是直线BC上的一动点（点D不与B、C重合），连接CE．

    （1）在图1中，当点D在边BC上时，求证：；

    （2）在图2中，当点D在边BC的延长线上时，结论是否还成立？若不成立，请猜想BC、CE、CD之间存在的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学七、八年级各选派10名选手参加学校举办的环保知识竞赛，计分采用10分制，选手得分均为整数，成绩达到6分或6分以上为合格，达到9分或10分为优秀．竞赛后，两支代表队选手的不完整成绩分布如下所示：

    （1）通过计算，补全表格；

    （2）有人说七年级的合格率、优秀率均高于八年级，所以七年级代表队成绩比八年级代表队好.但也有人说八年级代表队成绩比七年级代表队好．请你给出两条支持八年级代表队成绩较好的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，△ABC中，AD是高，AE平分∠BAC，∠B＝50°，∠C＝80°.求∠DAE的度数.

    查看答案和解析>>

    同步练习册答案