Question

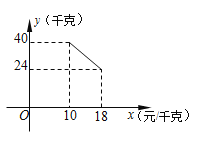
【题目】今年本市蜜桔大丰收，某水果商销售一种蜜桔，成本价为10元/千克，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于18元/千克，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克）之间的函数关系如图所示：

（1）求y与x之间的函数关系式；

（2）该经销商想要每天获得150元的销售利润，销售价应定为多少？

（销售利润=销售价－成本价）

Answer 1

【答案】（1）y=﹣2x+60；（2）销售价应定为15元。

【解析】试题分析：（1）设函数关系式y=kx+b，把（10，40），（18，24）代入求出k和b的值，即可得y与x之间的函数关系式；（2）根据销售利润=销售量×每一件的销售利润，列出方程，解一元二次方程求出x的值，根据实际情况对方程的解进行取舍即可.

试题解析：

1）设y与x之间的函数关系式y=kx+b，

把（10，40），（18，24）代入得：，解得，

∴y与x之间的函数关系式y=﹣2x+60；

（2）解：由题意得（x﹣10）（﹣2x+60）=150

x2-40x+375=0，

解得x1=15，x2=25（不合题意，舍去）

答：该经销商想要每天获得150元的销售利润，销售价应定为15元．