
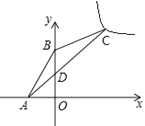
【题目】如图,在平面直角坐标系![]() 中,点A(
中,点A(![]() ,0),B(0,2),点C在第一象限,∠ABC=135°,AC交
,0),B(0,2),点C在第一象限,∠ABC=135°,AC交![]() 轴于D,CD=3AD,反比例函数
轴于D,CD=3AD,反比例函数![]() 的图象经过点C,则
的图象经过点C,则![]() 的值为_______.
的值为_______.
【答案】9
【解析】
过点A作AH⊥CB的延长线于点H,得到AH=BH=![]() =
=![]() ,根据已知条件得到B,H,A,O四点共圆,连接OH,推出H在第二象限角平分线上,作HM⊥x轴于M,HN⊥y轴于N,根据全等三角形的性质得到AM=BN=
,根据已知条件得到B,H,A,O四点共圆,连接OH,推出H在第二象限角平分线上,作HM⊥x轴于M,HN⊥y轴于N,根据全等三角形的性质得到AM=BN=![]() ,求得直线HB的解析式,于是得到结论.
,求得直线HB的解析式,于是得到结论.
解:∵点A(![]() ,0),B(0,2),
,0),B(0,2),
∴OA=1,OB=2,
∴![]() ;
;
如图,过点A作AH⊥CB的延长线于点H,
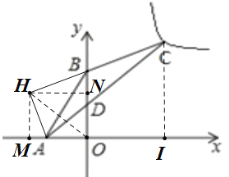
∵∠ABC=135°,
∴∠HBA=HAB=45°,
∴AH=BH=![]() =
=![]() ,
,
∵BH⊥AH,BO⊥AO,
∴B,H,A,O四点共圆,
连接OH,则∠BOH=∠BAH=45°,
∴H在第二象限角平分线上,
作HM⊥x轴于M,HN⊥y轴于N,
则四边形HMON是正方形,
∴HM=HN,
∵AH=BH,
∴Rt△HAM≌Rt△HBN,
∴AM=BN,
∵OM=ON,
∴AM=BN=![]() ,
,
∴H(![]() ,
,![]() ),
),
∴直线BH的解析式为y=![]() x+2,
x+2,
过C作CI⊥x轴于I,
∴OD∥CI,
∴![]() ,
,
∴OI=3AO=3,
把x=3代入y=![]() x+2得y=3,
x+2得y=3,
∴C点坐标为(3,3).
∵点C在反比例函数![]() 的图像上,
的图像上,
∴![]() ;
;
故答案为:9.


科目:初中数学 来源: 题型:
【题目】某社区决定把一块长![]() ,宽
,宽![]() 的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于
的矩形空地建成居民健身广场,设计方案如图,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于![]() ,不大于
,不大于![]() ,设绿化区较长边为
,设绿化区较长边为![]() ,活动区的面积为
,活动区的面积为![]() .为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于
.为了想知道出口宽度的取值范围,小明同学根据出口宽度不小于![]() ,算出
,算出![]() .
.
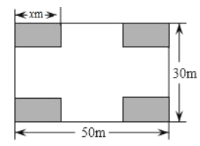
(1)求![]() 与
与![]() 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)求活动区的最大面积;
(3)预计活动区造价为50元/![]() ,绿化区造价为40元/
,绿化区造价为40元/![]() ,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
,若社区的此项建造投资费用不得超过72000元,求投资费用最少时活动区的出口宽度?
查看答案和解析>>
科目:初中数学 来源: 题型:
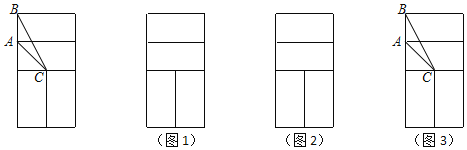
【题目】如图是四个全等的小矩形组成的图形,这些矩形的顶点称为格点.△ABC是格点三角形(顶点是格点的三角形)
(1)若每个小矩形的较短边长为1,则BC= ;
(2)①在图1、图2中分别画一个格点三角形(顶点是格点的三角形),使它们都与△ABC相似(但不全等),且图1,2中所画三角形也不全等).
②在图3中只用直尺(没有刻度)画出△ABC的重心M.(保留痕迹,点M用黑点表示,并注上字母M)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的二次函数y=x2-(2m-1)x+m2+3m+4.
(1)设二次函数y的图象与x轴的交点为A(x1,0),B(x2,0),且x12+x22=5,求二次函数的表达式;
(2)在(1)的条件下,设二次函数的图象与y轴交于点C,且在同一平面内,以A,B,C,P为顶点的四边形为平行四边形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在![]() 中,
中,![]() ,
,![]() ,
,![]() , 动点
, 动点![]() 从点
从点![]() 出发以每秒3个单位的速度运动至点
出发以每秒3个单位的速度运动至点![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒
秒![]() .
.
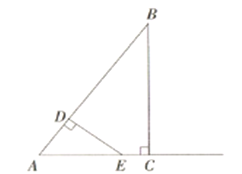
(1)线段![]() 长为 .(用含
长为 .(用含![]() 的代数式表示)
的代数式表示)
(2)若![]() 与
与![]() 的面积比为1:4时, 求
的面积比为1:4时, 求![]() 的值.
的值.
(3)设![]() 与
与![]() 重叠部分图形的周长为
重叠部分图形的周长为![]() , 求
, 求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当直线![]() 把
把![]() 分成的两部分图形中有一个是轴对称图形时,直接写出
分成的两部分图形中有一个是轴对称图形时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
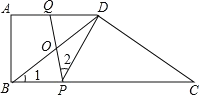
【题目】如图,在ABCD中,AD∥BC,∠A=90°,BD=DC,AB=6,AD=8,点P、Q分别为BC、AD上的动点,连接PQ,与BD相交于点O.
(1)当∠1=∠2时,求证:∠DOQ=∠DPC;
(2)当(1)的条件下,求证:DQ·PC=BD·DO;
(3)如果点P由点B向点C移动,每秒移动2个单位,同时点Q由点D向点A移动,每秒移动1个单位,设移动的时间为t秒,是否存在某一时刻,使得△BOP为直角三角形,如果存在,请直接写出t的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于2013年第30号强台风“海燕”的侵袭,致使多个城市受到影响.如图所示,A市位于台风中心M北偏东15°的方向上,距离![]() 千米,B市位于台风中心M正东方向
千米,B市位于台风中心M正东方向![]() 千米处. 台风中心以每小时30千米的速度沿MF向北偏东60°的方向移动(假设台风在移动的过程中的风速保持不变),距离台风中心60千米的圆形区域内均会受到此次强烈台风的影响.
千米处. 台风中心以每小时30千米的速度沿MF向北偏东60°的方向移动(假设台风在移动的过程中的风速保持不变),距离台风中心60千米的圆形区域内均会受到此次强烈台风的影响.
(1)A市、B市是否会受到此次台风的影响?说明理由.
(2)如果受到此次台风影响,该城市受到台风影响的持续时间为多少小时?
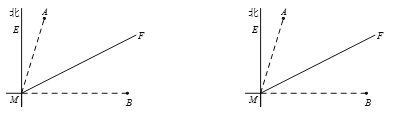
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于代数式![]() ,下列说法正确的是( )
,下列说法正确的是( )
①如果存在两个实数p≠q,使得ap2+bp+c=aq2+bq+c,则![]() ;
;
②存在三个实数m≠n≠s,使得am2+bm+c=an2+bn+c=as2+bs+c;
③如果ac<0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c;
④如果ac>0,则一定存在两个实数m<n,使am2+bm+c<0<an2+bn+c.
A.①B.③C.②④D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果制成如下两幅不完整的统计图:
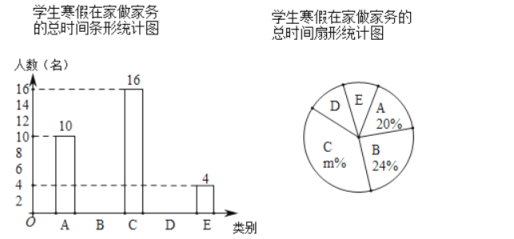
根据统计图提供的信息,解答下列问题:
(1)本次共调查了 名学生;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)扇形统计图中m的值是 ,类别D所对应的扇形圆心角的度数是 度;
(4)若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生寒假在家做家务的总时间不低于20小时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com