
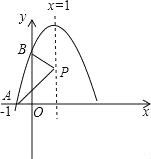
【题目】已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x,y轴的交点分别为A,B,P是其对称轴x=1上的动点,根据图中提供的信息,给出以下结论:①2a+b=0,②x=3是ax2+bx+3=0的一个根,③△PAB周长的最小值是![]() +3
+3![]() .其中正确的是( )
.其中正确的是( )
A. ①②③ B. 仅有①② C. 仅有①③ D. 仅有②③
【答案】A
【解析】
①根据对称轴方程求得a、b的数量关系;
②根据抛物线的对称性知抛物线与x轴的另一个交点的横坐标是3;
③利用两点间直线最短来求△PAB周长的最小值.
①根据图象知,对称轴是直线x=-![]() =1,则b=-2a,即2a+b=0,故①正确;
=1,则b=-2a,即2a+b=0,故①正确;
②根据图象知,点A的坐标是(-1,0),对称轴是x=1,则根据抛物线关于对称轴对称的性质知,抛物线与x轴的另一个交点的坐标是(3,0),所以x=3是ax2+bx+3=0的一个根,故②正确;
③如图所示,点A关于x=1对称的点是A′,即抛物线与x轴的另一个交点,
连接BA′与直线x=1的交点即为点P,则△PAB周长的最小值是(BA′+AB)的长度,
∵B(0,3),A′(3,0),
∴BA′=3![]() .即△PAB周长的最小值是3
.即△PAB周长的最小值是3![]() +
+![]() ,
,
故③正确.
综上所述,正确的结论是:①②③.
故选:A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】根据研究,人体内血乳酸浓度升高是运动后感觉疲劳的重要原因,运动员未运动时,体内血乳酸浓度水平通常在40mg/L以下;如果血乳酸浓度降到50mg/L以下,运动员就基本消除了疲劳,体育科研工作者根据实验数据,绘制了一副图象,它反映了运动员进行高强度运动后,体内血乳酸浓度随时间变化而变化的函数关系.
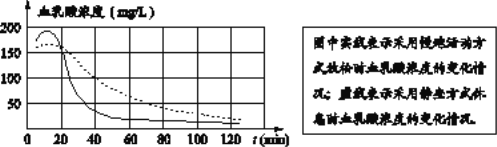
下列叙述正确的是
A. 运动后40min时,采用慢跑活动方式放松时的血乳酸浓度与采用静坐方式休息时的血乳酸浓度相同
B. 运动员高强度运动后最高血乳酸浓度大约为350mg/L
C. 运动员进行完剧烈运动,为了更快达到消除疲劳的效果,应该采用慢跑活动方式来放松
D. 采用慢跑活动方式放松时,运动员必须慢跑80min后才能基本消除疲劳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同,小明先从盒子里随机取出一个小球,记下数字为x,放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树形图表示出(x,y)的所有可能出现的结果;
(2)求小明、小华各取一次小球所确定的点(x,y)落在二次函数y=x2的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
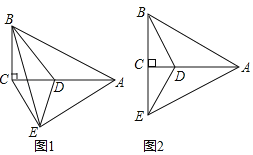
【题目】如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,将△ABD沿BD(对称轴)翻折,点A落在点E处,连接AE,CE.
(1)如图1,当∠AEC=90°时,求证:CD=AD;
(2)当点E落在BC边所在直线上,且∠AEC=60°时.
①猜想△BAE是什么三角形并证明;
②试求线段CD、AD之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
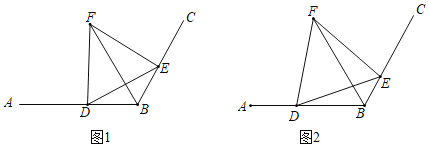
【题目】在图1、2中,已知∠ABC=120°,BD=2,点E为直线BC上的动点,连接DE,以DE为边向上作等边△DEF,使得点F在∠ABC内部,连接BF.
(1)如图1,当BD=BE时,∠EBF= ;
(2)如图2,当BD≠BE时,(1)中的结论是否成立?若成立,请予以证明,若不成立请说明理由;
(3)请直接写出线段BD,BE,BF之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若![]() ,则△A6B6A7的边长为( )
,则△A6B6A7的边长为( )
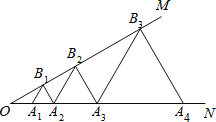
A.6B.12C.16D.32
查看答案和解析>>
科目:初中数学 来源: 题型:
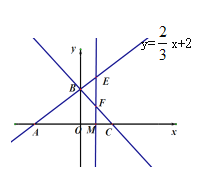
【题目】如图,一次函数y=![]() x+2的图象与x轴和y轴分别交于点A和B,直线y=kx+b经过点B与点C(2,0).
x+2的图象与x轴和y轴分别交于点A和B,直线y=kx+b经过点B与点C(2,0).
(1)点A的坐标为 ;点B的坐标为 ;
(2)求直线y=kx+b的表达式;
(3)在x轴上有一动点M(t,0),过点M做x轴的垂线与直线y=![]() x+2交于点E,与直线y=kx+b交于点F,若EF=OB,求t的值.
x+2交于点E,与直线y=kx+b交于点F,若EF=OB,求t的值.
(4)当点M(t,0)在x轴上移动时,是否存在t的值使得△CEF是直角三角形?若存在,直接写出t的值;若不存在,直接答不存在.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com