
【题目】如图,A,B两点的坐标分别为(6,0),(0,6),点P从点A出发,沿AB方向以每秒![]() 个单位的速度向终点B运动;同时动点Q从点B出发沿BO方向以每秒1个单位的速度向终点Q运动,将△PQO沿BO翻折,点P的对应点为点C,若四边形QPOC为菱形,则点C的坐标为________.
个单位的速度向终点B运动;同时动点Q从点B出发沿BO方向以每秒1个单位的速度向终点Q运动,将△PQO沿BO翻折,点P的对应点为点C,若四边形QPOC为菱形,则点C的坐标为________.
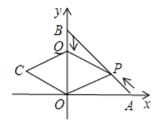
【答案】(-4,2)
【解析】
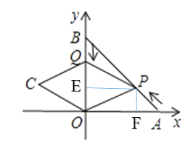
过P点作PE⊥y轴于E点,作PF⊥x轴于F点,根据翻折的性质,要使四边形QPOC为菱形,由于PC⊥OQ,只需QE=OE即可,设运动了t秒,则BQ=t,OQ=6-t,AP=![]() t,由等腰直角△APF得PF=t,故在矩形EPFO中,PF=EO=t,令OQ=2 EO,即可求出t,再求出Q点坐标即可.
t,由等腰直角△APF得PF=t,故在矩形EPFO中,PF=EO=t,令OQ=2 EO,即可求出t,再求出Q点坐标即可.
过P点作PE⊥y轴于E点,作PF⊥x轴于F点,
设运动了t秒,则BQ=t,OQ=6-t,AP=![]() t,由等腰直角△APF得PF=t,
t,由等腰直角△APF得PF=t,
要使四边形QPOC为菱形,由于PC⊥OQ,只需QE=OE即可,
在矩形EPFO中,PF=EO=t
OQ=2 EO,
即6-t=2t,解得t=2,故Q(0,4),E(0,2)P(4,2)
故C(-4,2)


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,……按照此规律继续下去,则S2019的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ ABCD中,E是AD边上一点,AD=4![]() ,CD=3,ED=
,CD=3,ED=![]() ,∠A=45.点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将
,∠A=45.点P,Q分别是BC,CD边上的动点,且始终保持∠EPQ=45°.将 ![]() CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为________.
CPQ沿它的一条边翻折,当翻折前后两个三角形组成的四边形为菱形时,线段BP的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在![]() ,
,![]() 两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是
两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是![]() 元,且随身听的单价比书包的单价的
元,且随身听的单价比书包的单价的![]() 倍少
倍少![]() 元.
元.
(1)求该同学看中的随身听和书包的单价各是多少元?
(2)某一天该同学上街,恰好赶上商家促销,超市![]() 所有商品打八五折销售,超市
所有商品打八五折销售,超市![]() 全场购物每满
全场购物每满![]() 元返购物券
元返购物券![]() 元销售(不足
元销售(不足![]() 元不返券,购物券全场通用),但他只带了
元不返券,购物券全场通用),但他只带了![]() 元钱,如果他只在一家超市购买看中的这两样商品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
元钱,如果他只在一家超市购买看中的这两样商品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
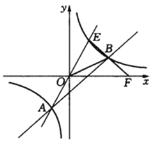
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于点A、E,AB交双曲线于另一点B(
交于点A、E,AB交双曲线于另一点B(![]() ,
,![]() ),连接EB并延长交x轴于点F.
),连接EB并延长交x轴于点F.
(1)![]() ;
;
(2)求直线AB的解析式;
(3)求△EOF的面积;
(4)若点P为坐标平面内一点,且以A,B,E,P为顶点的四边形是平行四边形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA,OD是⊙O半径.过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B.
(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为 3cm,求![]() 的长度.(结果保留π)
的长度.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) | 平均数(分) |
爱国班 | 85 | ||
求知班 | 100 | 85 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知爱国班复赛成绩的方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com