
ЁОЬтФПЁПЕчгАЙЋЫОЫцЛњЪеМЏСЫ2000ВПЕчгАЕФгаЙиЪ§ОнЃЌОЗжРрећРэЕУЕНШчБэЃК
ЕчгАРраЭ | ЕквЛРр | ЕкЖўРр | ЕкШ§Рр | ЕкЫФРр | ЕкЮхРр | ЕкСљРр |
ЕчгАВПЪ§ | 140 | 50 | 300 | 200 | 800 | 510 |
КУЦРТЪ |
|
|
|
|
|
|
зЂЃККУЦРТЪЪЧжИвЛРрЕчгАжаЛёЕУКУЦРЕФВПЪ§гыИУРрЕчгАЕФВПЪ§ЕФБШжЕЃЎ
![]() ШчЙћЕчгАЙЋЫОДгЪеМЏЕФЕчгАжаЫцЛњбЁШЁ1ВПЃЌФЧУДГщЕНЕФетВПЕчгАЪЧЛёЕУКУЦРЕФЕкЫФРрЕчгАЕФИХТЪЪЧ______ЃЛ
ШчЙћЕчгАЙЋЫОДгЪеМЏЕФЕчгАжаЫцЛњбЁШЁ1ВПЃЌФЧУДГщЕНЕФетВПЕчгАЪЧЛёЕУКУЦРЕФЕкЫФРрЕчгАЕФИХТЪЪЧ______ЃЛ
![]() ЕчгАЙЋЫОЮЊСЫдіМгЭЖзЪЛиБЈЃЌФтИФБфЭЖзЪВпТдЃЌетНЋЕМжТВЛЭЌРраЭЕчгАЕФКУЦРТЪЗЂЩњБфЛЏ
ЕчгАЙЋЫОЮЊСЫдіМгЭЖзЪЛиБЈЃЌФтИФБфЭЖзЪВпТдЃЌетНЋЕМжТВЛЭЌРраЭЕчгАЕФКУЦРТЪЗЂЩњБфЛЏ![]() МйЩшБэИёжажЛгаСНРрЕчгАЕФКУЦРТЪЪ§ОнЗЂЩњБфЛЏЃЌФЧУДФФРрЕчгАЕФКУЦРТЪдіМг
МйЩшБэИёжажЛгаСНРрЕчгАЕФКУЦРТЪЪ§ОнЗЂЩњБфЛЏЃЌФЧУДФФРрЕчгАЕФКУЦРТЪдіМг![]() ЃЌФФРрЕчгАЕФКУЦРТЪМѕЩй
ЃЌФФРрЕчгАЕФКУЦРТЪМѕЩй![]() ЃЌПЩЪЙИФБфЭЖзЪВпТдКѓзмЕФКУЦРТЪДяЕНзюДѓЃП
ЃЌПЩЪЙИФБфЭЖзЪВпТдКѓзмЕФКУЦРТЪДяЕНзюДѓЃП
Д№ЃК______ЃЎ
ЁОД№АИЁП![]() ЕкЮхРрЕчгАЕФКУЦРТЪдіМг0.1ЃЌЕкЖўРрЕчгАЕФКУЦРТЪМѕЩй0.1
ЕкЮхРрЕчгАЕФКУЦРТЪдіМг0.1ЃЌЕкЖўРрЕчгАЕФКУЦРТЪМѕЩй0.1
ЁОНтЮіЁП
(1)МЦЫуЕкЫФРрЕчгАжаЛёЕУКУЦРЕФЕчгАВПЪ§ЃЌДњШыЙЋЪНПЩЕУИХТЪ.
(2)ИљОнУПВПЕчгАЛёЕУКУЦРЕФВПЪ§зїГіКЯРэНЈвщ.
(1)ЕкЫФРрЕчгАжаЛёЕУКУЦРЕФЕчгАВПЪ§ЮЊЃК![]()
ГщЕНЕФетВПЕчгАЪЧЛёЕУКУЦРЕФЕкЫФРрЕчгАЕФИХТЪЪЧ![]()
(2)ЕкЮхРрЕчгАЕФЕчгАВПЪ§зюЖрЃЌЕкЖўРрЕчгАЕФЕчгАВПЪ§зюЩйЃЌдђЕкЮхРрЕчгАЕФКУЦРТЪдіМг0.1ЃЌЕкЖўРрЕчгАЕФКУЦРТЪМѕЩй0.1ЃЌПЩЪЙИФБфЭЖзЪВпТдКѓзмЕФКУЦРТЪДяЕНзюДѓ
ЙЪД№АИЮЊЃК(1). ![]() (2). ЕкЮхРрЕчгАЕФКУЦРТЪдіМг0.1ЃЌЕкЖўРрЕчгАЕФКУЦРТЪМѕЩй0.1
(2). ЕкЮхРрЕчгАЕФКУЦРТЪдіМг0.1ЃЌЕкЖўРрЕчгАЕФКУЦРТЪМѕЩй0.1



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМбМбЕїЫСЫЦпФъМЖ400УћбЇЩњЕНаЃЕФЗНЪНЃЌИљОнЕїВщНсЙћЛцжЦГіЭГМЦЭМЕФвЛВПЗжШчЭМЃК
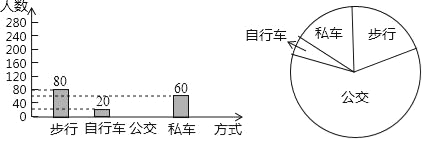
ЃЈ1ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉЧѓЩШаЮЭГМЦЭМжаБэЪОЁАВНааЁБЕФЩШаЮдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЙРМЦдк3000УћбЇЩњжаГЫЙЋНЛЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
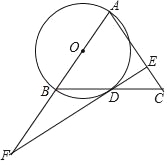
ЁОЬтФПЁПвбжЊЁбOЕФАыОЖЮЊ10ЃЌдВаФOЕНЯвABЕФОрРыЮЊ5ЃЌдђЯвABЫљЖдЕФдВжмНЧЕФЖШЪ§ЪЧЃЈЁЁЁЁЃЉ
A. 30Ёу B. 60Ёу C. 30ЁуЛђ150Ёу D. 60ЁуЛђ120Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЁЂBЕФзјБъЗжБ№ЮЊЃЈ0ЃЌ4ЃЉЁЂЃЈ4ЃЌ0ЃЉЃЌЕуCдкЕквЛЯѓЯоФкЃЌЁЯBAC=90ЁуЃЌAB=2ACЃЌКЏЪ§y=![]() ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§ЕуCЃЌНЋЁїABCбиxжсЕФе§ЗНЯђЯђгвЦНвЦmИіЕЅЮЛГЄЖШЃЌЪЙЕуAЧЁКУТфдкКЏЪ§y=
ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§ЕуCЃЌНЋЁїABCбиxжсЕФе§ЗНЯђЯђгвЦНвЦmИіЕЅЮЛГЄЖШЃЌЪЙЕуAЧЁКУТфдкКЏЪ§y=![]() ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌдђmЕФжЕЮЊЃЈЁЁЁЁЃЉ
ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌдђmЕФжЕЮЊЃЈЁЁЁЁЃЉ

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕШбќ![]() жаЃЌ
жаЃЌ![]() ЃЌвд
ЃЌвд![]() ЮЊжБОЖзї
ЮЊжБОЖзї![]() НЛБп
НЛБп![]() гкЕу
гкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌбгГЄ
ЃЌбгГЄ![]() НЛ
НЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁбOЕФжБОЖAB=4cmЃЌЕуCЮЊЯпЖЮABЩЯвЛЖЏЕуЃЌЙ§ЕуCзїABЕФДЙЯпНЛЁбOгкЕуDЃЌEЃЌСЌНсADЃЌAE.ЩшACЕФГЄЮЊxcmЃЌЁїADEЕФУцЛ§ЮЊycm2.
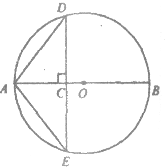
аЁЖЋИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§yЫцздБфСПxЕФБфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОП.
ЯТУцЪЧаЁЖЋЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
(1)ЭЈЙ§ШЁЕуЁЂЛЭМЁЂВтСПЁЂЗжЮіЃЌЕУЕНСЫyгыxЕФМИзщЖдгІжЕЃЌШчЯТБэЃК
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y/cm2 | 0 | 0.7 | 1.7 | 2.9 | 4.8 | 5.2 | 4.6 | 0 |
(2)ШчЭМЃЌНЈСЂЦНУцжБНЧзјБъЯЕ![]() ЃЌУшГівдВЙШЋКѓЕФБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
ЃЌУшГівдВЙШЋКѓЕФБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ

(3)НсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕБЁїADEЕФУцЛ§ЮЊ4cm2ЪБЃЌACЕФГЄЖШдМЮЊ___________cm.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
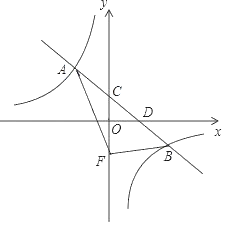
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§yЃНЉ![]() x+bЕФЭМЯѓгыЗДБШР§КЏЪ§yЃН
x+bЕФЭМЯѓгыЗДБШР§КЏЪ§yЃН![]() ЃЈkЁй0ЃЉЭМЯѓНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌгыxжсНЛгкЕуDЃЌЦфжаAЕузјБъЮЊЃЈЉ2ЃЌ3ЃЉЃЎ
ЃЈkЁй0ЃЉЭМЯѓНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌгыxжсНЛгкЕуDЃЌЦфжаAЕузјБъЮЊЃЈЉ2ЃЌ3ЃЉЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§НтЮіЪНЃЎ
ЃЈ2ЃЉШєНЋЕуCбиyжсЯђЯТЦНвЦ4ИіЕЅЮЛГЄЖШжСЕуFЃЌСЌНгAFЁЂBFЃЌЧѓЁїABFЕФУцЛ§ЃЎ
ЃЈ3ЃЉИљОнЭМЯѓЃЌжБНгаДГіВЛЕШЪНЉ![]() x+bЃО
x+bЃО![]() ЕФНтМЏЃЎ
ЕФНтМЏЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЙ§A(Ѓ2, 0), C(0, 6)СНЕуЕФХзЮяЯпyЃНЃ![]() x2ЃЋaxЃЋbгыxжсНЛгкСэвЛЕуBЃЌЕуDЪЧХзЮяЯпЕФЖЅЕуЃЎ
x2ЃЋaxЃЋbгыxжсНЛгкСэвЛЕуBЃЌЕуDЪЧХзЮяЯпЕФЖЅЕуЃЎ
ЃЈ1ЃЉЧѓaЁЂbЕФжЕЃЛ
ЃЈ2ЃЉЕуPЪЧxжсЩЯЕФвЛИіЖЏЕуЃЌЙ§PзїжБЯпl//ACНЛХзЮяЯпгкЕуQЃЎЫцзХЕуPЕФдЫЖЏЃЌШєвдAЁЂPЁЂQЁЂCЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧыжБНгаДГіЗћКЯЬѕМўЕФЕуQЕФзјБъЃЛ
(3)дкжБЯпACЩЯЪЧЗёДцдквЛЕуMЃЌЪЙЁїBDMЕФжмГЄзюаЁЃЌШєДцдкЃЌЧыевГіЕуMВЂЧѓГіЕуMЕФзјБъЃЎШєВЛДцдкЃЌЧыЫЕУїРэгЩЁЃ


БИгУЭМ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
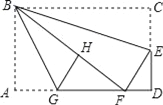
ЁОЬтФПЁПШчЭМЃЌдкОиаЮжНЦЌABCDжаЃЌAB=6ЃЌBC=10ЃЌЕуEдкCDЩЯЃЌНЋЁїBCEбиBEелЕўЃЌЕуCЧЁТфдкБпADЩЯЕФЕуFДІЃЛЕуGдкAFЩЯЃЌНЋЁїABGбиBGелЕўЃЌЕуAЧЁТфдкЯпЖЮBFЩЯЕФЕуHДІЃЌгаЯТСаНсТлЃК
ЂйЁЯEBG=45ЁуЃЛЂкЁїDEFЁзЁїABGЃЛЂлSЁїABG=![]() SЁїFGHЃЛЂмAG+DF=FGЃЎ
SЁїFGHЃЛЂмAG+DF=FGЃЎ
Цфжае§ШЗЕФЪЧ__ЃЎЃЈАбЫљгае§ШЗНсТлЕФађКХЖМбЁЩЯЃЉ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com