练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．等腰△ABC中，AB、AC的长是关于x的方程x2-7x+12=0的两根，求△ABC的周长．

    分析 把方程左边利用十字相乘法分解因式，根据两数积为0，两数至少有一个为0化为两个一元一次方程，分别求出两方程的解得到原方程的解为4或3，然后根据4为腰，4为底边分两种情况考虑，分别根据三角形的边角关系判断满足题意的底边和腰，进而求出三角形的周长．

    解答 解：x2-7x+12=0，
    因式分解得：（x-4）（x-3）=0，
    可得：x-4=0或x-3=0，
    解得：x1=4，x2=3，
    若4为腰，3为底边，三角形三边分别为3，4，4，此时三角形周长为3+4+4=11；
    若4为底边，3为腰，三角形三边分别为4，3，3，此时三角形周长为4+3+3=10．

    点评 本题从边的方面考查三角形，涉及分类讨论的思想方法．求三角形的周长，不能盲目地将三边长相加起来，而应养成检验三边长能否组成三角形的好习惯，把不符合题意的舍去．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．一个盒子中有标有数字1，2，3，4，5，6，7，8，9，10，11的11张卡片，小聪随意从中拿卡片，规定：若拿一张卡片，则相邻的必拿，例如拿卡片2，则必拿卡片1，3，则至少拿4张偶数字的卡片的拿法（　　）种．
    A．6B．8C．9D．10

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，在矩形ABCD中，BC=6，CD=3，将△BCD沿对角线BD翻折，点C落在点C′处，BC′交AD于点E，求线段DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：（$\frac{1}{3}$-$\frac{1}{5}$）×（$\frac{1}{5}$）-2÷|-$\frac{1}{3}$|+（-$\frac{1}{5}$）0+（-0.25）2007×42007．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．看图填空：已知如图，AD⊥BC于D，EG⊥BC与G，∠E=∠1，求证：AD平分∠BAC．
    证明：∵AD⊥BC于D，EG⊥BC于G（已知）
    ∴∠ADC=90°，∠EGC=90°（垂直的定义）
    ∴∠ADC=∠EGC
    ∴AD∥EG（同位角相等，两直线平行　　）
    ∴∠1=∠2（两直线平行，内错角相等）
    ∠E=∠3（两直线平行，同位角相等）
    又∵∠E=∠1（已知）
    ∴∠2=∠3
    ∴AD平分∠BAC（角平分线的定义）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

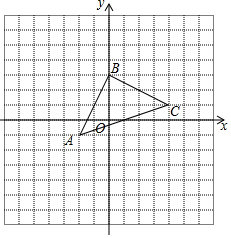    16．如图，三角形ABC中，A，B，C的坐标分别为（-2，-1），（0，3），（4，1），三角形ABC中任意一点P（x0，y0）经过平移后对应点为P1（x0+2，y0+1），将三角形ABC作同样的平移得到三角形A1B1C1．
    （1）在图中画出三角形A1B1C1，并直接写出A1，B1，C1的坐标；
    （2）求三角形A1B1C1的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．在求1+3+32+33+34+35+36+37+38的值时，李敏发现：从第二个加数起每一个加数都是前一个加数的3倍，于是她假设：S=1+3+32+33+34+35+36+37+38①，
    然后在①式的两边都乘以3，得：3S=3+32+33+34+35+36+37+38+39②，
    ②-①得，3S-S=39-1，即2S=39-1，所以S=$\frac{{3}^{9}-1}{2}$．
    得出答案后，爱动脑筋的张红想：如果把“3”换成字母a（a≠0且a≠1），能否求出1+a+a2+a3+a4+…+a2017的值？如能求出，其正确答案是$\frac{{a}^{2017}-1}{a-1}$（a≠0且a≠1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．为了了解本班学生关注“两会”新闻的情况，“两会”期间，小明对本班全体同学一周内收看“两会”新闻的次数作调查，调查结果制成统计图如图所示（其中男生一周内收看4次的人数没有标出）：

    请你根据以上信息，解答下列问题：
    （1）该班女生有3人，该班女生一周内收看“两会”新闻次数的中位数是3次；
    （2）对于某个群体，我们把一周内收看“两会”新闻次数高于4次的人数占该群体总人数的百分比叫做该群体对“两会”新闻的“关注指数”，如果该班男生对“两会”新闻的“关注指数”为60%，试求该班男生有多少人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．某县教育局为了丰富初中学生的大课间活动，要求各学校开展形式多样的阳光体育活动．某中学就“学生体育活动兴趣爱好”的问题，随机调查了本校某班的学生，并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图：

    （1）在这次调查中，喜欢篮球项目的同学有5人，在扇形统计图中，“乒乓球”的百分比为20%，如果学校有800名学生，估计全校学生中有80人喜欢篮球项目．
    （2）请将条形统计图补充完整．
    （3）在被调查的学生中，喜欢篮球的有2名女同学，其余为男同学．现要从中随机抽取2名同学代表班级参加校篮球队，请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率．

    查看答案和解析>>

    同步练习册答案