
ЁОЬтФПЁПаЁУїЮЊСЫЭЈЙ§УшЕуЗЈзїГіКЏЪ§y=x2-x+1ЕФЭМЯѓЃЌЯШШЁздБфСПxЕФ7ИіжЕТњзуЃКx2-x1=x3-x2=Ё=x7-x6=dЃЌдйЗжБ№ЫуГіЖдгІЕФyжЕЃЌСаГіБэЃК

МЧm1=y2-y1ЃЌm2=y3-y2ЃЌm3=y4-y3ЃЌm4=y5-y4ЃЌЁЃЛs1=m2-m1ЃЌs2=m3-m2ЃЌs3=m4-m3ЃЌЁ
ЃЈ1ЃЉХаЖЯs1ЁЂs2ЁЂs3жЎМфЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєНЋКЏЪ§ЁАy=x2-x+1ЁБИФЮЊЁАy=ax2+bx+cЃЈaЁй0ЃЉЁБЃЌСаГіБэЃК

ЦфЫћЬѕМўВЛБфЃЌХаЖЯs1ЁЂs2ЁЂs3жЎМфЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉаЁУїЮЊСЫЭЈЙ§УшЕуЗЈзїГіКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓЃЌСаГіБэЃК

гЩгкаЁУїЕФДжаФЃЌБэжагавЛИіyжЕЫуДэСЫЃЌЧыжИГіЫуДэЕФyжЕЃЈжБНгаДД№АИЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉs1=s2=s3ЃЎРэгЩМћНтЮіЃЛЃЈ2ЃЉs1=s2=s3ЃЎРэгЩМћНтЮіЃЛЃЈ3ЃЉ412ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃК1ЃЉЃЈ2ЃЉПЩЗжБ№БэЪОГіs1ЃЌs2ЃЌs3ЕФжЕЃЌШЛКѓНјааБШНЯМДПЩЃЎ
ЃЈ3ЃЉИљОнЃЈ1ЃЉЃЈ2ЃЉЕУГіЕФЙцТЩЃЌНјааХаЖЯМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉs1=s2=s3ЃЎm1=y2-y1=3-1=2ЃЌ
ЭЌРэm2=4ЃЌm3=6ЃЌm4=8ЃЎ
Ёрs1=m2-m1=4-2=2ЃЌ
ЭЌРэs2=2ЃЌs3=2ЃЎ
Ёрs1=s2=s3ЃЎ
ЃЈ2ЃЉs1=s2=s3ЃЎ
ЗНЗЈвЛЃКm1=y2-y1=ax22+bx2+c-ЃЈax12+bx1+cЃЉ
=d[aЃЈx2+x1ЃЉ+b]ЃЎ
m2=y3-y2=ax32+bx3+c-ЃЈax22+bx2+cЃЉ
=d[aЃЈx3+x2ЃЉ+b]ЃЎ
ЭЌРэm3=d[aЃЈx4+x3ЃЉ+b]ЃЎ
m4=d[aЃЈx5+x4ЃЉ+b]ЃЎ
s1=m2-m1=d[aЃЈx3+x2ЃЉ+b]-d[aЃЈx2+x1ЃЉ+b]
=2ad2ЃЎ
ЭЌРэs2=2ad2ЃЎ
s3=2ad2ЃЎ
Ёрs1=s2=s3ЃЎ
ЗНЗЈЖўЃКЁпx2-x1=dЃЌ
Ёрx2=x1+dЃЌ
Ёрm1=y2-y1=aЃЈx1+dЃЉ2+bЃЈx1+dЃЉ+c-ЃЈax12+bx1+cЃЉ
=d[aЃЈ2x1+dЃЉ+b]ЃЎ
гжЁпx3-x2=dЃЌ
Ёрx3=x2+dЃЌ
Ёрm2=y3-y2=aЃЈx2+dЃЉ2+bЃЈx2+dЃЉ+c-ЃЈax22+bx2+cЃЉ
=d[aЃЈ2x2+dЃЉ+b]ЃЎ
ЭЌРэm3=d[aЃЈ2x3+dЃЉ+b]ЃЎ
m4=d[aЃЈ2x4+dЃЉ+b]ЃЎ
s1=m2-m1=d[aЃЈ2x2+dЃЉ+b]-d[aЃЈ2x1+dЃЉ+b]
=2ad2ЃЎ
ЭЌРэs2=2ad2ЃЎs3=2ad2ЃЎ
Ёрs1=s2=s3ЃЎ
ЃЈ3ЃЉ412ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈжаЃЌе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A. Ш§ЕуШЗЖЈвЛИідВ B. Ш§НЧаЮгаЧвжЛгавЛИіЭтНгдВ
C. ЫФБпаЮЖМгавЛИіЭтНгдВ D. дВгаЧвжЛгавЛИіФкНгШ§НЧаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЉ3ЃЈxЉ2yЃЉ+4ЃЈxЉ2yЃЉЕФНсЙћЪЧЃЈЁЁЁЁЃЉ
A. xЉ2y B. x+2y C. ЉxЉ2y D. Љx+2y
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌABЪЧЁбOЕФжБОЖЃЌAB=8ЃЌЕуCдкЁбOЕФАыОЖOAЩЯдЫЖЏЃЌPCЁЭABЃЌДЙзуЮЊCЃЌPC=5ЃЌPTЮЊЁбOЕФЧаЯпЃЌЧаЕуЮЊT.
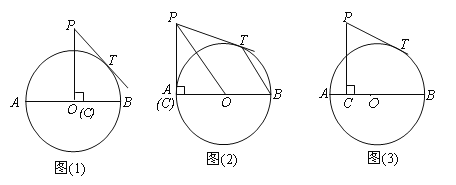
ЂХШчЭМЂХЃЌЕБCЕудЫЖЏЕНOЕуЪБЃЌЧѓPTЕФГЄ;
ЂЦШчЭМЂЦЃЌЕБCЕудЫЖЏЕНAЕуЪБЃЌСЌНсPOЁЂBTЃЌЧѓжЄЃКPOЁЮBT;
ЂЧШчЭМЂЧЃЌЩш![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНМА
ЕФКЏЪ§ЙиЯЕЪНМА![]() ЕФзюаЁжЕ.
ЕФзюаЁжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCжаЃЌADЮЊBCБпЩЯЕФЕФжаЯпЃЌдђSЁїABD= SЁїADC.

ЪЕМљЬНОП
ЃЈ1ЃЉдкЭМ2жаЃЌEЁЂFЗжБ№ЮЊОиаЮABCDЕФБпADЁЂBCЕФжаЕуЃЌдђSвѕКЭSОиаЮABCDжЎМфТњзуЕФЙиЯЕЪНЮЊ ЃЛ
ЃЈ2ЃЉдкЭМ3жаЃЌEЁЂFЗжБ№ЮЊЦНааЫФБпаЮABCDЕФБпADЁЂBCЕФжаЕуЃЌдђSвѕКЭSЦНааЫФБпаЮABCDжЎМфТњзуЕФЙиЯЕЪНЮЊ ЃЛ
ЃЈ3ЃЉдкЭМ4жаЃЌEЁЂFЗжБ№ЮЊШЮвтЫФБпаЮABCDЕФБпADЁЂBCЕФжаЕуЃЌдђSвѕКЭSЫФБпаЮABCDжЎМфТњзуЕФЙиЯЕЪНЮЊ ЃЛ
НтОіЮЪЬтЃК
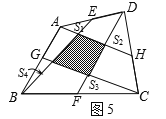
ЃЈ4ЃЉдкЭМ5жаЃЌEЁЂGЁЂFЁЂHЗжБ№ЮЊШЮвтЫФБпаЮABCDЕФБпADЁЂABЁЂBCЁЂCDЕФжаЕуЃЌВЂЧвЭМжавѕгАВПЗжЕФУцЛ§ЮЊ20ЦНЗНУзЃЌЧѓЭМжаЫФИіаЁШ§НЧаЮЕФУцЛ§КЭЪЧЖрЩйЃПМДЧѓS1+ S2+ S3+ S4=ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌOЮЊе§ЗНаЮABCDЕФжааФЃЌBEЦНЗжЁЯDBCЃЌНЛDCгкЕуEЃЌбгГЄBCЕНЕуFЃЌЪЙCF=CEЃЌСЌНсDFЃЌНЛBEЕФбгГЄЯпгкЕуGЃЌСЌНсOGЃЎ

(1)ЧѓжЄЃКЁїBCEЁеЁїDCFЃК
(2)OGгыBFгаЪВУДЪ§СПЙиЯЕ?жЄУїФуЕФНсТлЃЛ
(3)ШєGE![]() GB=4-2
GB=4-2![]() ЃЌЧѓе§ЗНаЮABCDЕФУцЛ§ЃЎ
ЃЌЧѓе§ЗНаЮABCDЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ3ЗжЃЉвбжЊ2aЉ3b2=5ЃЌдђ10Љ2a+3b2ЕФжЕЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСљЖрБпаЮЕФФкНЧКЭЮЊЃЈ ЃЉ
A. 180Ёу B. 360Ёу C. 720Ёу D. 1080Ёу
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com