
ЎҫМвДҝЎҝ¶ЁТеЈәФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ЕЧОпПЯ![]() ЈЁ
ЈЁ![]() Ј©УлЦұПЯ
Ј©УлЦұПЯ![]() Ҫ»УЪөг
Ҫ»УЪөг![]() Ўў
Ўў![]() ЈЁөг
ЈЁөг![]() ФЪөг
ФЪөг![]() УТұЯЈ©Ј¬Ҫ«ЕЧОпПЯ
УТұЯЈ©Ј¬Ҫ«ЕЧОпПЯ![]() СШЦұПЯ
СШЦұПЯ![]() ·ӯХЫЈ¬·ӯХЫЗ°әуБҪЕЧОпПЯөД¶Ҙөг·ЦұрОӘөг
·ӯХЫЈ¬·ӯХЫЗ°әуБҪЕЧОпПЯөД¶Ҙөг·ЦұрОӘөг![]() Ўў
Ўў![]() Ј¬ОТГЗҪ«БҪЕЧОпПЯЦ®јдРОіЙөД·вұХНјРОіЖОӘҫӘПІПЯЈ¬ЛДұЯРО
Ј¬ОТГЗҪ«БҪЕЧОпПЯЦ®јдРОіЙөД·вұХНјРОіЖОӘҫӘПІПЯЈ¬ЛДұЯРО![]() іЖОӘҫӘПІЛДұЯРОЈ¬¶ФҪЗПЯ
іЖОӘҫӘПІЛДұЯРОЈ¬¶ФҪЗПЯ![]() Ул
Ул![]() Ц®ұИіЖОӘҫӘПІ¶ИЈЁDegree of surpriseЈ©Ј¬јЗЧч
Ц®ұИіЖОӘҫӘПІ¶ИЈЁDegree of surpriseЈ©Ј¬јЗЧч![]() .
.
ЈЁ1Ј©ИзНјЈЁ1Ј©ЕЧОпПЯ![]() СШЦұПЯ
СШЦұПЯ![]() ·ӯХЫәуөГөҪҫӘПІПЯ.Фтөг
·ӯХЫәуөГөҪҫӘПІПЯ.Фтөг![]() Чшұк Ј¬өг
Чшұк Ј¬өг![]() Чшұк Ј¬ҫӘПІЛДұЯРО
Чшұк Ј¬ҫӘПІЛДұЯРО![]() КфУЪЛщС§№эөДДДЦЦМШКвЖҪРРЛДұЯРОЈҝ Ј¬
КфУЪЛщС§№эөДДДЦЦМШКвЖҪРРЛДұЯРОЈҝ Ј¬![]() ОӘ .
ОӘ .
ЈЁ2Ј©Из№ыЕЧОпПЯ![]() ЈЁ
ЈЁ![]() Ј©СШЦұПЯ
Ј©СШЦұПЯ![]() ·ӯХЫәуЛщөГҫӘПІПЯөДҫӘПІ¶ИОӘ1Ј¬Зу
·ӯХЫәуЛщөГҫӘПІПЯөДҫӘПІ¶ИОӘ1Ј¬Зу![]() өДЦө.
өДЦө.
ЈЁ3Ј©Из№ыЕЧОпПЯ![]() СШЦұПЯ
СШЦұПЯ![]() ·ӯХЫәуЛщөГөДҫӘПІПЯФЪ
·ӯХЫәуЛщөГөДҫӘПІПЯФЪ![]() КұЈ¬ЖдЧоёЯөгөДЧЭЧшұкОӘ16Ј¬Зу
КұЈ¬ЖдЧоёЯөгөДЧЭЧшұкОӘ16Ј¬Зу![]() өДЦөІўЦұҪУРҙіцҫӘПІ¶И
өДЦөІўЦұҪУРҙіцҫӘПІ¶И![]() .
.
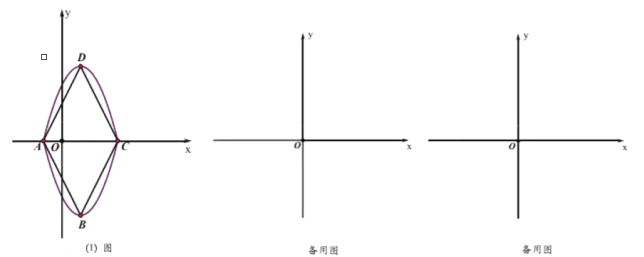
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»
Ј»![]() Ј»БвРОЈ»2Ј»ЈЁ2Ј©
Ј»БвРОЈ»2Ј»ЈЁ2Ј©![]() Ј»ЈЁ3Ј©
Ј»ЈЁ3Ј©![]() Ј¬
Ј¬![]() »т
»т![]() Ј¬
Ј¬![]() .
.
ЎҫҪвОцЎҝ
ЈЁ1Ј©өұy=0КұҝЙЗуіцөгAЧшұкОӘ![]() Ј¬BЧшұкОӘ
Ј¬BЧшұкОӘ![]() Ј¬AB=4Ј¬ёщҫЭЛДұЯРОЛДұЯПаөИҝЙЦӘёГЛДұЯРООӘБвРОЈ¬УЙ
Ј¬AB=4Ј¬ёщҫЭЛДұЯРОЛДұЯПаөИҝЙЦӘёГЛДұЯРООӘБвРОЈ¬УЙ![]() ҝЙЦӘЕЧОпПЯ¶ҘөгЧшұкОӘЈЁ1Ј¬-4Ј©Ј¬ЛщТФB
ҝЙЦӘЕЧОпПЯ¶ҘөгЧшұкОӘЈЁ1Ј¬-4Ј©Ј¬ЛщТФB![]() Ј¬AB=8Ј¬јҙҝЙөГөҪ
Ј¬AB=8Ј¬јҙҝЙөГөҪ![]() ОӘ2Ј»
ОӘ2Ј»
ЈЁ2Ј©ҫӘПІ¶ИОӘ1јҙ![]() Ј¬АыУГЕЧОпПЯҪвОцКҪ·ЦұрЗуіцёчөгЧшұкЈ¬ҙУ¶шөГөҪACәНBDөДіӨЈ¬јЖЛгјҙҝЙЗуіцmЈ»
Ј¬АыУГЕЧОпПЯҪвОцКҪ·ЦұрЗуіцёчөгЧшұкЈ¬ҙУ¶шөГөҪACәНBDөДіӨЈ¬јЖЛгјҙҝЙЗуіцmЈ»
ЈЁ3Ј©ПИЗуіц¶ҘөгЧшұк![]() Ј¬¶ФіЖЦбОӘЦұПЯ
Ј¬¶ФіЖЦбОӘЦұПЯ![]() Ј¬МЦВЫ¶ФіЖЦбЦұПЯ
Ј¬МЦВЫ¶ФіЖЦбЦұПЯ![]() КЗ·сФЪ
КЗ·сФЪ![]() Хвёц·¶О§ДЪЈ¬·Ц3ЦРЗйҝц·ЦұрЗуіцЧоҙуЦөОӘ16КЗmөДЦө.
Хвёц·¶О§ДЪЈ¬·Ц3ЦРЗйҝц·ЦұрЗуіцЧоҙуЦөОӘ16КЗmөДЦө.
ҪвЈәЈЁ1Ј©ФЪЕЧОпПЯ![]() ЙПЈ¬
ЙПЈ¬
өұy=0КұЈ¬![]() Ј¬
Ј¬
ҪвөГЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬
ЎЯөг![]() ФЪөг
ФЪөг![]() УТұЯЈ¬
УТұЯЈ¬
ЎаAөгөДЧшұкОӘ![]() Ј¬BөгөДЧшұкОӘ
Ј¬BөгөДЧшұкОӘ![]() Ј»
Ј»
ЎаAB=4Ј¬
ЎЯ![]()
Ўа¶ҘөгBөДЧшұкОӘ![]() Ј¬
Ј¬
УЙУЪBD№ШУЪxЦб¶ФіЖЈ¬
ЎаDөДЧшұкОӘ![]() Ј¬
Ј¬
ЎаBD=8Ј¬
НЁ№эЕЧОпПЯөД¶ФіЖРФөГөҪAB=BCЈ¬
УЦУЙУЪ·ӯХЫЈ¬өГөҪAB=BC=AD=CDЈ¬
ЎаҫӘПІЛДұЯРО![]() ОӘБвРОЈ»
ОӘБвРОЈ»
![]() Ј»
Ј»
ЈЁ2Ј©УЙМвТвөГЈә![]()
![]() өД¶ҘөгЧшұк
өД¶ҘөгЧшұк![]() Ј¬
Ј¬![]()
ҪвөГЈә![]() Ј¬Ўа
Ј¬Ўа![]()
![]()
Ўа![]() Ј¬
Ј¬![]()
ЈЁ3Ј©ЕЧОпПЯөД¶ҘөгОӘ![]() Ј¬¶ФіЖЦбОӘЦұПЯЈә
Ј¬¶ФіЖЦбОӘЦұПЯЈә![]()
ўЩ![]() јҙ
јҙ![]() КұЈ¬
КұЈ¬![]() Ј¬өГ
Ј¬өГ![]()
Ўа![]()
ўЪ![]() јҙ
јҙ![]() КұЈ¬
КұЈ¬![]() КұЈ¬¶ФУҰҫӘПІПЯЙПЧоёЯөгөДәҜКэЦө
КұЈ¬¶ФУҰҫӘПІПЯЙПЧоёЯөгөДәҜКэЦө![]()
![]() Ј¬Ўа
Ј¬Ўа![]() ЈЁЙбИҘЈ©Ј»
ЈЁЙбИҘЈ©Ј»![]()
Ўа![]()
ўЫ![]() јҙ
јҙ![]() КұРОіЙІ»БЛҫӘПІПЯЈ¬№КІ»ҙжФЪ
КұРОіЙІ»БЛҫӘПІПЯЈ¬№КІ»ҙжФЪ![]()
ЧЫЙПЛщКцЈ¬![]() Ј¬
Ј¬![]() »т
»т![]() Ј¬
Ј¬![]()




| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
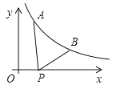
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘ![]() Ј¬
Ј¬![]() ОӘ·ҙұИАэәҜКэ
ОӘ·ҙұИАэәҜКэ![]() НјПуЙПөДБҪөгЈ¬¶Ҝөг
НјПуЙПөДБҪөгЈ¬¶Ҝөг![]() ФЪ
ФЪ![]() ЦбХэ°лЦбЙПФЛ¶ҜЈ¬өұПЯ¶О
ЦбХэ°лЦбЙПФЛ¶ҜЈ¬өұПЯ¶О![]() УлПЯ¶О
УлПЯ¶О![]() Ц®ІоҙпөҪЧоҙуКұЈ¬өг
Ц®ІоҙпөҪЧоҙуКұЈ¬өг![]() өДЧшұкКЗЈЁ Ј©
өДЧшұкКЗЈЁ Ј©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ACКЗЎСOөДЦұҫ¶Ј¬ПТBDЎНAOУЪEЈ¬Б¬ҪУBCЈ¬№эөгOЧчOFЎНBCУЪFЈ¬ИфBD=8cmЈ¬AE=2cmЈ¬ФтOFөДіӨ¶ИКЗЈЁЎЎЎЎЈ©

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
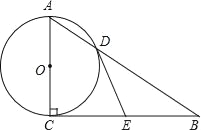
ЎҫМвДҝЎҝИзНјЈ¬ФЪRtЎчABCЦРЈ¬ЎПACB=90ЎгЈ¬ТФACОӘЦұҫ¶өДЎСOУлABұЯҪ»УЪөгDЈ¬№эөгDЧчЎСOөДЗРПЯЈ®Ҫ»BCУЪөгEЈ®
ЈЁ1Ј©ЗуЦӨЈәBE=EC
ЈЁ2Ј©МоҝХЈәўЩИфЎПB=30ЎгЈ¬AC=2![]() Ј¬ФтDB=ЎЎ ЎЎЈ»
Ј¬ФтDB=ЎЎ ЎЎЈ»
ўЪөұЎПB=ЎЎ ЎЎ¶ИКұЈ¬ТФOЈ¬DЈ¬EЈ¬CОӘ¶ҘөгөДЛДұЯРОКЗХэ·ҪРОЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
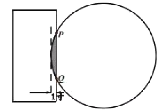
ЎҫМвДҝЎҝЎ¶ҫЕХВЛгКхЎ·КЗТ»ұҫЦР№ъДЛЦБ¶«·ҪКАҪзЧоО°ҙуөДТ»ұҫЧЫәПРФКэС§ЦшЧчЈ¬ұкЦҫЧЕЦР№ъ№ЕҙъКэС§РОіЙБЛНкХыөДМеПө.Ў°ФІІДВсұЪЎұКЗЎ¶ҫЕХВЛгКхЎ·ЦРөДТ»ёцОКМвЈәЎ°ҪсУРФІІДЈ¬ВсФЪұЪЦРЈ¬І»ЦӘҙуРЎЈ¬ТФҫвҫвЦ®Ј¬ЙоТ»ҙзЈ¬ҫвөАіӨТ»іЯЈ¬ОКҫ¶јёәОЈҝЎұЦмАПКҰёщҫЭФӯОДМвТвЈ¬»ӯіцБЛФІІДҪШГжНјИзНјЛщКҫЈ¬ТСЦӘЈәҫвҝЪЙоОӘ1ҙзЈ¬ҫвөА![]() іЯЈЁ1іЯ=10ҙзЈ©Ј¬ФтёГФІІДөДЦұҫ¶іӨОӘЈЁ Ј©
іЯЈЁ1іЯ=10ҙзЈ©Ј¬ФтёГФІІДөДЦұҫ¶іӨОӘЈЁ Ј©
A.26ҙзB.25ҙзC.13ҙзD.![]() ҙз
ҙз
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘЕЧОпПЯ![]() УлxЦбҪ»УЪөгAЎўBЈ¬УлyЦб·ЦұрҪ»УЪөгCЈ¬ЖдЦРөг
УлxЦбҪ»УЪөгAЎўBЈ¬УлyЦб·ЦұрҪ»УЪөгCЈ¬ЖдЦРөг![]() Ј¬өг
Ј¬өг![]() Ј¬ЗТ
Ј¬ЗТ![]() .
.
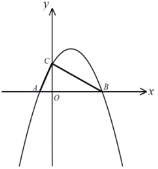
ЈЁ1Ј©ЗуЕЧОпПЯөДҪвОцКҪЈ»
ЈЁ2Ј©өгPКЗПЯ¶ОABЙПТ»¶ҜөгЈ¬№эPЧч![]() Ҫ»BCУЪDЈ¬өұ
Ҫ»BCУЪDЈ¬өұ![]() Гж»эЧоҙуКұЈ¬ЗуөгPөДЧшұкЈ»
Гж»эЧоҙуКұЈ¬ЗуөгPөДЧшұкЈ»
ЈЁ3Ј©өгMКЗО»УЪПЯ¶ОBCЙП·ҪөДЕЧОпПЯЙПТ»өгЈ¬өұ![]() ЗЎәГөИУЪ
ЗЎәГөИУЪ![]() ЦРөДДіёцҪЗКұЈ¬ЗуөгMөДЧшұк.
ЦРөДДіёцҪЗКұЈ¬ЗуөгMөДЧшұк.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝПВБРЛө·ЁХэИ·өДКЗЈЁЎЎЎЎЈ©
A. БЛҪвОТКРКРГсЦӘПюЎ°АсИГРРИЛЎұҪ»НЁРВ№жөДЗйҝцЈ¬ККәПИ«ГжөчІй
B. јЧЎўТТБҪИЛМшФ¶іЙјЁөД·ҪІо·ЦұрОӘ![]() Ј¬
Ј¬![]() Ј¬ЛөГчТТөДМшФ¶іЙјЁұИјЧОИ¶Ё
Ј¬ЛөГчТТөДМшФ¶іЙјЁұИјЧОИ¶Ё
C. Т»ЧйКэҫЭ2Ј¬2Ј¬3Ј¬4өДЦЪКэКЗ2Ј¬ЦРО»КэКЗ2.5
D. ҝЙДЬРФКЗ1%өДКВјюФЪТ»ҙОКФСйЦРТ»¶ЁІ»»б·ўЙъ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ЦұПЯlЈәyЈҪx©Ғ1УлxЦбҪ»УЪөгAЈ¬ИзНјЛщКҫТАҙОЧчХэ·ҪРОA1B1C1OЎўХэ·ҪРОA2B2C2C1ЎӯЎўХэ·ҪРОAnBnnCn+1Ј¬К№өГөгA1ЎўA2ЎўA3ЎўЎӯФЪЦұПЯlЙПЈ¬өгC1ЎўC2ЎўC3ЎўЎӯФЪyЦбХэ°лЦбЙПЈ¬ФтөгBөДЧшұкКЗ_____Ј¬өгBnөДЧшұкКЗ_____Ј®
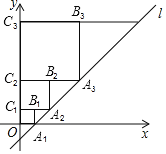
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
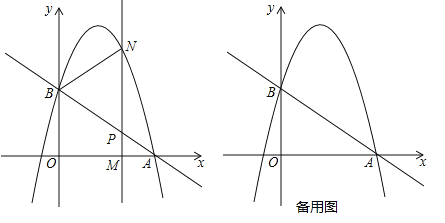
ЎҫМвДҝЎҝИзНјЈ¬ЕЧОпПЯ![]() №эөг
№эөг![]() әН
әН![]() Ј¬өг
Ј¬өг![]() ОӘПЯ¶О
ОӘПЯ¶О![]() ЙПТ»ёц¶Ҝөг(өг
ЙПТ»ёц¶Ҝөг(өг![]() Улөг
Улөг![]() І»ЦШәП)Ј¬№эөг
І»ЦШәП)Ј¬№эөг![]() Ччҙ№ЦұУЪ
Ччҙ№ЦұУЪ![]() ЦбөДЦұПЯУлЦұПЯ
ЦбөДЦұПЯУлЦұПЯ![]() әНЕЧОпПЯ·ЦұрҪ»УЪөг
әНЕЧОпПЯ·ЦұрҪ»УЪөг![]() Ј®
Ј®
ЈЁ1Ј©ЗуҙЛЕЧОпПЯөДҪвОцКҪЈ»
ЈЁ2Ј©Ифөг![]() КЗ
КЗ![]() өДЦРөгЈ¬ФтЗуөг
өДЦРөгЈ¬ФтЗуөг![]() өДЧшұкЈ»
өДЧшұкЈ»
ЈЁ3Ј©ИфТФөг![]() ОӘ¶ҘөгөДИэҪЗРОУл
ОӘ¶ҘөгөДИэҪЗРОУл![]() ПаЛЖЈ¬ЗлЦұҪУРҙіцөг
ПаЛЖЈ¬ЗлЦұҪУРҙіцөг![]() өДЧшұкЈ®
өДЧшұкЈ®
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com