
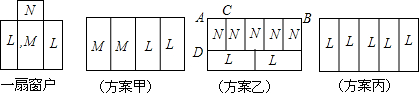
���� ��1����5��N�Ͳ����ij���2m���AC�ij����ɣ�Ҳ����L�Ͳ����Ŀ�������2L=5N���L�Ͳ����ij������AD���ɣ�
��2��һ��������ҪM�Ͳ���Ƭ1�飬N�Ͳ���Ƭ1�飬L�Ͳ���Ƭ2�飬����x���ȴ�����������������������x����������ѡ�����ɣ�
��3������y���ȴ�������������������̣�̽�ֵó�y����ֵ���ɣ�
��� �⣺��1��AC=2��5=0.4m��
AD=2��2-0.4=0.6m��
��2��M��N��L�Ͳ���Ƭ�ij������ֱ�Ϊ��1m��0.6m��0.6m��0.4m��1m��0.4m��
����x���ȴ������������
��x-4����1��0.6+1��0.4��2x+0.6��0.4x=7��2��1
��ã�x=10��
7�������Ҫ�ָ��M��N��L�Ͳ���Ƭ������Ϊ6��10��20��
��˷�����3�飬������2�飬������2�飻
��3������y���ȴ������������
��y-50����1��0.6+1��0.4��2y+0.6��0.4y=a��2��1
��a=$\frac{41}{50}$y-15��
����Ϊ20��a��70����yȡ50��100��150��
���a=26��67��
�ʴ�Ϊ26��67��
���� ���⿼��һԪһ�η��̣���Ԫһ�η��̵�ʵ�����ã��ҳ���Ŀ�̺���������ϵ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����A������Ϊ��-1��0������B��a��-2����ֱ��y=2x-4�ϣ�
��ͼ����A������Ϊ��-1��0������B��a��-2����ֱ��y=2x-4�ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 60�� | B�� | 90�� | C�� | 120�� | D�� | 135�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���߳��ֱ�Ϊ1��2��3��4������2015��2016�������ε�����һ����ͼ����Ӱ���ֵ����������ʾ��1+2+3��+n=$\frac{1}{2}$n��n+1����
��ͼ���߳��ֱ�Ϊ1��2��3��4������2015��2016�������ε�����һ����ͼ����Ӱ���ֵ����������ʾ��1+2+3��+n=$\frac{1}{2}$n��n+1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �Խ�����ƽ�ֵ��ı�����ƽ���ı��� | |
| B�� | �����εĶԽ�����ƽ���Ҵ�ֱ | |
| C�� | ���εĶԽ�������һ��ഹֱ | |
| D�� | �Խ�����ƽ������ȵ��ı����Ǿ��� | |
| E�� | �Խ�����ƽ������ȵ��ı����Ǿ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com