
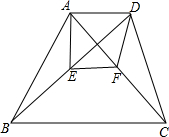
 已知四边形ABCD,E,F分别是BD,AC的中点,若四边形ABCD的面积是2016,则四边形AEFD的面积为多少?
已知四边形ABCD,E,F分别是BD,AC的中点,若四边形ABCD的面积是2016,则四边形AEFD的面积为多少? 分析 连接EC,根据三角形的中线把三角形分为面积相等的两个三角形求出四边形AECD的面积,再进一步求出四边形AEFD的面积.
解答 解: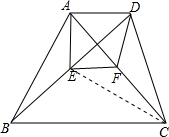 连接EC,
连接EC,
∵E是BD的中点,
S△ABE=S△ADE,S△BEC=S△DEC,
∴S四边形AECD=$\frac{1}{2}$S△四边形ABCD=1008,
∵F是AC的中点,
∴S△AEF=$\frac{1}{2}$S△AEC,S△ADF=$\frac{1}{2}$S△ADC,
∴四边形AEFD的面积为$\frac{1}{2}$×S四边形AECD=504.
点评 本题考查的是三角形的面积的计算,掌握三角形的中线把三角形分为面积相等的两个三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
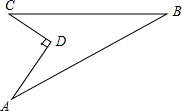 如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?
如图,某住宅小区在施工过程中留下了一块空地,已知AD=8米,CD=6米,∠ADC=90°,AB=26米,BC=24米,小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问用该草坪铺满这块空地共需花费多少元?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
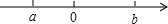 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com