

| 解:(1)=; | |
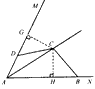
| (2)仍然成立,理由: 如图(1)过C作CE⊥AM于E,CF⊥AN于F,则∠CEA=∠CFA=90°, ∵AC平分∠MAN,∠MAN=120°, ∴∠MAC=∠NAC=60°, 又∵AC=AC, ∴△AEC≌△AFC ∴AE=AF,CE=CF ∵在Rt△CEA中,∠EAC=60° ∴∠ECA=30° ∴AC=2AE ∴AE+AF=2AE=AC, ∴ED+DA+AE=AC, ∵∠ABC+∠ADC=180°,∠CDE+∠ADC=180°, ∴∠CDE=∠CBF, 又∵CE=CF,∠CED=∠CFB, ∴△CED≌△CFB, ∴ED=FB, ∴FB+DA+AF=AC, ∴AB+AD=AC; |
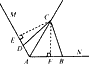 |
(3)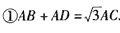 理由:如图(2)方法同(2)可证△AGC≌△AHC ∴AG=AH, ∵∠MAN=60°, ∴∠GAC=∠HAC=30°, ∴AG=AH=  , ,∴AG+AH=  , ,∴GD+DA+AH=  ,方法同(2)可证△GDC≌△HBC, ,方法同(2)可证△GDC≌△HBC,∴DG=HB, ∴HB+DA+AH= 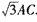 , ,∴AD+AB= 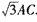 ; ;②2cos  。 。 |
 |


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
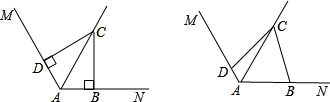
查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北黄陂北片学校八年级上第一次月考数学试卷(带解析) 题型:解答题
已知∠MAN,AC平分∠MAN。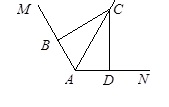
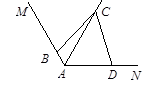
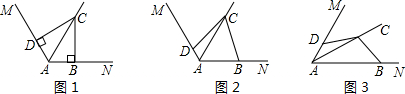
⑴在图1中,若∠MAN=120°,∠ABC=∠ADC=90°求证:AB+AD=AC;
⑵在图2中,若∠MAN=120°,∠ABC+∠ADC=180°,则⑴中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏东台创新学校九年级上学期第二次阶段测试数学试卷(解析版) 题型:解答题
已知∠MAN,AC平分∠MAN.
(1)在图1中,若∠MAN=120°,∠ABC=∠ADC=90°,我们可得结论:AB+AD=AC;

在图2中,若∠MAN=120°,∠ABC+∠ADC=180°,则上面的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;

【解】
(2)在图3中:(只要填空,不需要证明).

①若∠MAN=60°,∠ABC+∠ADC=180°,则AB+AD= AC;
②若∠MAN=α(0°<α<180°),∠ABC+∠ADC=180°,则AB+AD= AC(用含α的三角函数表示)。
查看答案和解析>>
科目:初中数学 来源:2011-2012学年湖北黄陂北片学校八年级上第一次月考数学试卷(解析版) 题型:解答题
已知∠MAN,AC平分∠MAN。
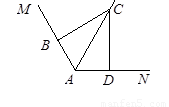

⑴在图1中,若∠MAN=120°,∠ABC=∠ADC=90°求证:AB+AD=AC;
⑵在图2中,若∠MAN=120°,∠ABC+∠ADC=180°,则⑴中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com