
 ��ƽ��ֱ������ϵ�У���A��ԭ��O������ÿ�������ƶ�2����λ���Ȼ������ƶ�1����λ���ȣ�
��ƽ��ֱ������ϵ�У���A��ԭ��O������ÿ�������ƶ�2����λ���Ȼ������ƶ�1����λ���ȣ�| A�ӵ�O�����ƶ����� | ���ܵ���ĵ������ |
| 1�� | ��0��2������1��0�� |
| 2�� | ��0��4������1��2������2��0�� |
| 3�� | ��0��6������1��4������2��2������3��0�� |
���� ��1�����ݵ��ƽ���ص����ÿ��ƽ�ƺ�P���λ�ü��ɣ�
��2�����ȸ���P��ƽ��һ�κ�ĵ������������˵�ĺ�������ʽ�����ٸ��ݺ���ͼ��ƽ�Ƶ����ʽ�ɣ�
��3�����B������Ϊ��x��y�������B������꣬�ó�n�ķ��̣��ٸ��ݵ�B������Ϊ���������ɽ��н��
��� �⣺��1����ͼ��ʾ��
| P�ӵ�O����ƽ�ƴ��� | ���ܵ���ĵ� ������ |
| 1�� | ��0��2������1��0�� |
| 2�� | ��0��4������1��2������2��0�� |
| 3�� | ��0��6������1��4������2��2������3��0�� |
���� ���⿼�����һ�κ�����ͼ���뼸�α任����֪����ͼ��ƽ�Ƶķ����ǽ�����Ĺؼ���


 һ����������ϵ�д�
һ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��AB=AC=AD����˵����
��ͼ��ʾ��AB=AC=AD����˵�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
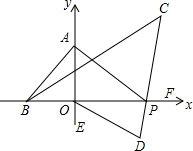 ��ͼ����ƽ��ֱ������ϵ�У���ABO=2��BAO��PΪx��������һ���㣬BCƽ�֡�ABP��PCƽ�֡�APF��ODƽ�֡�POE
��ͼ����ƽ��ֱ������ϵ�У���ABO=2��BAO��PΪx��������һ���㣬BCƽ�֡�ABP��PCƽ�֡�APF��ODƽ�֡�POE�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����ij��˾һ������ԡ��ˮ���ˮ��y�������빩ˮʱ��x���֣��ĺ�����ϵ��
��ͼ��ʾ����ij��˾һ������ԡ��ˮ���ˮ��y�������빩ˮʱ��x���֣��ĺ�����ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 1883�꣬���ж������������Σ��������ж������������ϵ�λ�����߶ο�ʼ�����ж�ȡ�����м�����֮һ���ﵽ��һ�Σ�Ȼ���ÿһ�����µ�����֮һ�߶���ȡ�����м�����֮һ���ﵽ�ڶ��Σ������ظ���һ���̣����µ�����㼯�ͳ������ж�������ͼ�ǿ��ж�������������Σ����ﵽ��n����ʱ�����µ������߶εij���֮��Ϊ��������
1883�꣬���ж������������Σ��������ж������������ϵ�λ�����߶ο�ʼ�����ж�ȡ�����м�����֮һ���ﵽ��һ�Σ�Ȼ���ÿһ�����µ�����֮һ�߶���ȡ�����м�����֮һ���ﵽ�ڶ��Σ������ظ���һ���̣����µ�����㼯�ͳ������ж�������ͼ�ǿ��ж�������������Σ����ﵽ��n����ʱ�����µ������߶εij���֮��Ϊ��������| A�� | $\frac{2n}{3}$ | B�� | $\frac{2n}{3}$ | C�� | ${��\frac{2}{3}��^n}$ | D�� | ${��\frac{2}{3}��^{n-1}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com