
【题目】如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.
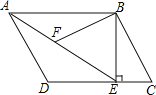
(1)求证:△ABF∽△EAD;
(2)若AB=4,BE=3,AD=![]() ,求BF的长.
,求BF的长.
【答案】(1)证明见解析;(2)BF=![]() .
.
【解析】
试题分析:(1)求三角形相似就要得出两组对应的角相等,已知了∠BFE=∠C,根据等角的补角相等可得出∠ADE=∠AFB,根据AB∥CD可得出∠BAF=∠AED,这样就构成了两三角形相似的条件.
(2)根据(1)的相似三角形可得出关于AB,AE,AD,BF的比例关系,有了AD,AB的长,只需求出AE的长即可.可在直角三角形ABE中用勾股定理求出AE的长,这样就能求出BF的长了.
(1)证明:在平行四边形ABCD中,
∵∠D+∠C=180°,AB∥CD,
∴∠BAF=∠AED.
∵∠AFB+∠BFE=180°,∠D+∠C=180°,∠BFE=∠C,
∴∠AFB=∠D,
∴△ABF∽△EAD.
(2)解:∵BE⊥CD,AB∥CD,
∴BE⊥AB.
∴∠ABE=90°.
∴AE=![]() =
=![]() =5.
=5.
∵△ABF∽△EAD,
∴![]() =
=![]() ,
,
∴![]() =
=![]() .
.
∴BF=![]() .
.


科目:初中数学 来源: 题型:
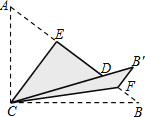
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. “打开电视,正在播放河南新闻节目”是必然事件
B. 某种彩票中奖概率为10%是指买十张一定有一张中奖
C. 神舟飞船反射前需要对零部件进行抽样调查
D. 了解某种节能灯的使用寿命适合抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列算式中,正确的是( )
A. 2x+2y=4xy B. 2a2+2a3=2a5 C. 4a2﹣3a2=1 D. ﹣2ba2+a2b=﹣a2b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 一组数据的众数、中位数和平均数不可能是同一个数
B. 一组数据的平均数既不可能大于,也不可能小于这组数据中的所有数据
C. 一组数据的中位数可能与这组数据的任何数据都不相等
D. 一组数据中的众数可能有多个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8,AC=4,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F.
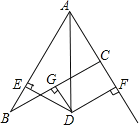
(1)求证:BE=CF;
(2)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】)如图,在△ABC中,D是BC边上的中点,F、E分别是AD及其延长线上的点,CF∥BE。

(1)试说明△BDE≌△CDF
(2)请连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com