
【题目】我们规定:若 ![]() =(a,b),
=(a,b), ![]() =(c,d),则
=(c,d),则 ![]() =ac+bd.如
=ac+bd.如 ![]() =(1,2),
=(1,2), ![]() =(3,5),则
=(3,5),则 ![]() =1×3+2×5=13.
=1×3+2×5=13.
(1)已知 ![]() =(2,4),
=(2,4), ![]() =(2,﹣3),求
=(2,﹣3),求 ![]() ;
;
(2)已知 ![]() =(x﹣a,1),
=(x﹣a,1), ![]() =(x﹣a,x+1),求y=
=(x﹣a,x+1),求y= ![]() ,问y=
,问y= ![]() 的函数图象与一次函数y=x﹣1的图象是否相交,请说明理由.
的函数图象与一次函数y=x﹣1的图象是否相交,请说明理由.
【答案】
(1)
解:∵ ![]() =(2,4),
=(2,4), ![]() =(2,﹣3),
=(2,﹣3),
∴ ![]() =2×2+4×(﹣3)=﹣8
=2×2+4×(﹣3)=﹣8
(2)
解:∵ ![]() =(x﹣a,1),
=(x﹣a,1), ![]() =(x﹣a,x+1),
=(x﹣a,x+1),
∴y= ![]() =(x﹣a)2+(x+1)
=(x﹣a)2+(x+1)
=x2﹣(2a﹣1)x+a2+1
∴y=x2﹣(2a﹣1)x+a2+1
联立方程:x2﹣(2a﹣1)x+a2+1=x﹣1,
化简得:x2﹣2ax+a2+2=0,
∵△=b2﹣4ac=﹣8<0,
∴方程无实数根,两函数图象无交点
【解析】此题主要考查了根的判别式以及新定义,正确得出y与x之间的函数关系式是解题关键.(1)直接利用 ![]() =(a,b),
=(a,b), ![]() =(c,d),则
=(c,d),则 ![]() =ac+bd,进而得出答案;(2)利用已知的出y与x之间的函数关系式,再联立方程,结合根的判别式求出答案.
=ac+bd,进而得出答案;(2)利用已知的出y与x之间的函数关系式,再联立方程,结合根的判别式求出答案.
【考点精析】利用一次函数的性质和求根公式对题目进行判断即可得到答案,需要熟知一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
![]()
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD,AD上,则AP+PQ的最小值为( ) 
A.2 ![]()
B.![]()
C.2 ![]()
D.3 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为3cm2 , E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于 cm.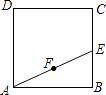
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O(0,0),A(0,﹣6),B(8,0)三点在⊙P上.
(1)求圆的半径及圆心P的坐标;
(2)M为劣弧 ![]() 的中点,求证:AM是∠OAB的平分线;
的中点,求证:AM是∠OAB的平分线;
(3)连接BM并延长交y轴于点N,求N,M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在某商店购买商品A、B共两次,这两次购买商品A、B的数量和费用如表:
购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) | |
第一次购物 | 4 | 3 | 93 |
第二次购物 | 6 | 6 | 162 |
若小丽需要购买3个商品A和2个商品B,则她要花费( )
A.64元
B.65元
C.66元
D.67元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com