
 如图,在△ABC,AB=AC=2,△ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是2$\sqrt{3}$-2.
如图,在△ABC,AB=AC=2,△ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是2$\sqrt{3}$-2. 分析 首先求得BC的长度,然后由两点之间线段最短可知:当点B、Q、C、A′在同一条直线上时,BA′的长度最小,然后根据BA′=BC-A′C求解即可.
解答 解:如图所示过点A作AD⊥BC于点D.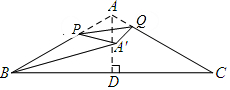
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD=$\frac{1}{2}$×120°=60°,BD=DC.
∴sin∠BAD=$\frac{BD}{AB}$,即$\frac{BD}{2}$=$\frac{\sqrt{3}}{2}$.
∴BD=$\sqrt{3}$.
∴BC=2$\sqrt{3}$.
由翻折的性质可知:A′Q=AQ
∵AQ+NQ=AC=2,
∴A′Q+QC=2.
要求BA′的最小值,只需BA′+A′Q+QC有最小值,由两点之间线段最短可知:当点B、Q、C、A′在同一条直线上时,BA′的长度最小.
如图所示: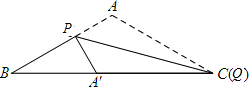
由翻折的性质可知:A′C=AC.
∴BA′=BC-A′C=2$\sqrt{3}$-2.
故答案是:2$\sqrt{3}$-2.
点评 本题主要考查的是翻折的性质、特殊度数的锐角三角函数值、线段的性质的应用,明确当点B、Q、C、A′在同一条直线上时,BA′的长度最小是解题的关键.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{24}$ | B. | $\sqrt{27}$ | C. | $\sqrt{96}$ | D. | $\sqrt{0.5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m$<\frac{1}{4}$ | B. | m$≤\frac{1}{4}$ | C. | m$≥\frac{1}{4}$ | D. | m$≤\frac{1}{4}$且m≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com