
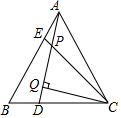
 如图,△ABC是等边三角形,E,D分别是边AB,BC上的点,AE=BD,AD和CE交于点P,CQ⊥AD于点Q,若CP=8,PQ=4.
如图,△ABC是等边三角形,E,D分别是边AB,BC上的点,AE=BD,AD和CE交于点P,CQ⊥AD于点Q,若CP=8,PQ=4. 分析 先利用等边三角形的性质得AB=AC,∠BAC=∠B=60°,则利用“SAS”可证明△ABD≌△CAE,所以∠BAD=∠ACE,再证明∠QPC=∠EAC=60°,然后根据含30度的直角三角形三边的关系求PQ的长.
解答 解:∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠B=60°,
在△ABD和△CAE中
$\left\{\begin{array}{l}{AB=CA}\\{∠B=∠CAE}\\{BD=AE}\end{array}\right.$
∴△ABD≌△CAE,
∴∠BAD=∠ACE,
∴∠QPC=∠PCA+∠PAC=∠PAE+∠PAC=∠EAC=60°,
∵CQ⊥AD,
∴∠PQC=90°,
在Rt△PQC中,∵∠PCQ=90°-60°=30°,
∴PQ=$\frac{1}{2}$PC=$\frac{1}{2}$×8=4.
故答案为4.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.也考查了等边三角形的性质.


科目:初中数学 来源: 题型:填空题
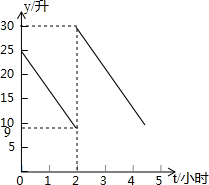 张师傅驾车从甲地到乙地,两地相距S千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以同样的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.张师傅途中加油21升.
张师傅驾车从甲地到乙地,两地相距S千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以同样的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.张师傅途中加油21升.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 观察图中尺规作图痕迹,下列说法错误的是( )
观察图中尺规作图痕迹,下列说法错误的是( )| A. | OE平分∠AOB | B. | 点C、D到OE的距离不一定相等 | ||
| C. | OC=OD | D. | 点E到OA、OB的距离一定相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com