
【题目】如图,正方形![]() 和正方形
和正方形![]() 中,点
中,点![]() 在CG上,BC=1,CE=3,H是AF的中点,那么
在CG上,BC=1,CE=3,H是AF的中点,那么![]() 的长是( )
的长是( )

A.![]() B.
B.![]() C.
C.![]() D.2
D.2
【答案】B
【解析】
延长BA和FG交于点M,连接AC和CF,根据正方形的性质可得四边形MADG为矩形,GM=AB=BC=CD=1, GC=CE=GF=3,∠ACD=∠GCF=45°,从而求出MA、MF、∠M和∠ACF,根据勾股定理即可求出AF,然后根据直角三角形斜边上的中线等于斜边的一半即可求出结论.
解:延长BA和FG交于点M,连接AC和CF

∵正方形![]() 和正方形
和正方形![]() 中,BC=1,CE=3,
中,BC=1,CE=3,
∴四边形MADG为矩形,GM=AB=BC=CD=1, GC=CE=GF=3,∠ACD=∠GCF=45°
∴MA=GD=GC-CD=2,MF=GM+GF=4,∠M=90°,∠ACF=∠ACD+∠GCF=90°
根据勾股定理可得AF=![]()
∵H是AF的中点,
∴CH=![]() AF=
AF=![]()
故选B.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.

(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在平行四边形ABCD中,E为BC边上一点,连结AE、BD且AE=AB

(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形的斜边![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 与原点重合,点
与原点重合,点![]() 的坐标是
的坐标是![]() ,且
,且![]() ,若将
,若将![]() 绕着点
绕着点![]() 旋转后30°,点
旋转后30°,点![]() 和
和![]() 点分别落在点
点分别落在点![]() 和点
和点![]() 处,那么直线
处,那么直线![]() 的解析式是__________.
的解析式是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与应用:
阅读1:a、b为实数,且a>0,b>0,因为 ![]() ,所以
,所以 ![]() ,从而
,从而 ![]() (当a=b时取等号).
(当a=b时取等号).
阅读2:函数 ![]() (常数m>0,x>0),由阅读1结论可知:
(常数m>0,x>0),由阅读1结论可知: ![]()
![]() ,所以当
,所以当 ![]() 即
即 ![]() 时,函数
时,函数 ![]() 的最小值为
的最小值为 ![]() .
.
阅读理解上述内容,解答下列问题:
(1)问题1:已知一个矩形的面积为4,其中一边长为x,则另一边长为 ![]() ,周长为
,周长为 ![]() ,求当x=时,周长的最小值为 .
,求当x=时,周长的最小值为 .
(2)问题2:已知函数y1=x+1(x>-1)与函数y2=x2+2x+17(x>-1),当x=时, ![]() 的最小值为 .
的最小值为 .
(3)问题3:某民办学习每天的支出总费用包含以下三个部分:一是教职工工资6400元;二是学生生活费每人10元;三是其他费用.其中,其他费用与学生人数的平方成正比,比例系数为0.01.当学校学生人数为多少时,该校每天生均投入最低?最低费用是多少元?(生均投入=支出总费用÷学生人数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G. 
(1)求证:△ADB≌△CEA;
(2)若BD=9,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图所示,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3, 已知A(1,3),A1 (2,3), A2 (4,3), A3 (8,3),B(2,0), B1 (4,0), B2 (8,0), B3 (16,0),观察每次变换前后的三角形有何变化,找出规律,按此变换规律将△OA3B3变换成△OAnBn, ,则An的坐标是_______ ,Bn的坐标是_________ .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,山脚下有一棵树AB,小强从点B沿山坡向上走50m到达点D,用高为1.5m的测角仪CD测得树顶为10°,已知山坡的坡脚为15°,则树AB的高=(精确到0.1m)(已知sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,sin15°≈0.26,cos15°≈0.97,tan15°≈0.27).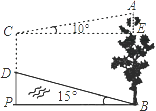
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com