练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．下列图形，线段、等边三角形、矩形、圆、正五边形中，既是轴对称图形，又是中心对称图形的个数是（　　）
    A．2B．3C．4D．5

    分析 根据轴对称图形与中心对称图形的概念求解即可．

    解答 解：线段是轴对称图形，也是中心对称图形；
    等边三角形是轴对称图形，不是中心对称图形；
    矩形是轴对称图形，也是中心对称图形；
    圆是轴对称图形，也是中心对称图形；
    正五边形是轴对称图形，不是中心对称图形；
    故既是轴对称图形，又是中心对称图形的个数是3．
    故选B．

    点评 本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合；中心对称图形的关键是要寻找对称中心，旋转180度后两部分重合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    2．一个长方形在平面直角坐标系中三个顶点的坐标为（3，2），（-1，2），（3，-1），则第四个顶点的坐标为（-1，-1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．已知二元一次方程组$\left\{\begin{array}{l}x-2y=1\\ x+3y=6\end{array}\right.$的解是$\left\{\begin{array}{l}x=3\\ y=1\end{array}\right.$，那么一次函数y=$\frac{1}{2}x-\frac{1}{2}$与y=$-\frac{1}{3}x+2$的图象的交点坐标为（3，1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

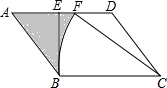    20．如图，平行四边形ABCD中，BE⊥AD于点E，以C为圆心，BC长为半径画弧，恰好过AD的中点F，若BC=4，BE=2，则图中阴影部分的面积为6-$\frac{4}{3}$π．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．计算：|-3|-（-1）2016×（π-3）0-$\root{3}{27}$+（$\frac{1}{2}$）-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图，下列条件中不能判定a∥b的是（　　）
    A．∠1+∠4=180°B．∠1=∠3C．∠1=∠2D．∠2=∠5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：$\sqrt{18}$-2sin45°+$\sqrt{（3-π）^{2}}$+（$\frac{1}{3}$）-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

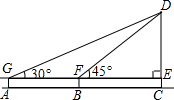    1．某校数学兴趣小组的同学用学到的解直角三角形的知识，测量聊城摩天轮圆心D到地面AC的高度CD，如图，在空地的A处，他们利用测角仪器测得CD顶端的仰角为30°，沿AC方向前进40米到达B处，又测得CD顶端的仰角为45°，已知测交仪器的高度为1.2米，求摩天轮圆心到地面的高度．（$\sqrt{3}$≈1.732，精确到0.1米）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．已知：关于x的二次函数y=x2+bx+c经过点（-1，0）和（2，6）．
    （1）求b和c的值．
    （2）若点A（n，y1），B（n+1，y2），C（n+2，y3）都在这个二次函数的图象上，问是否存在整数n，使$\frac{1}{{y}_{1}}$+$\frac{1}{{y}_{2}}$+$\frac{1}{{y}_{3}}$=$\frac{3}{10}$？若存在，请求出n；若不存在，请说明理由．
    （3）若点P是二次函数图象在y轴左侧部分上的一个动点，将直线y=-2x沿y轴向下平移，分别交x轴、y轴于C、D两点，若以CD为直角边的△PCD与△OCD相似，请求出所有符合条件点P的坐标．

    查看答案和解析>>

    同步练习册答案