
 18、在下面的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=6
18、在下面的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=6科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
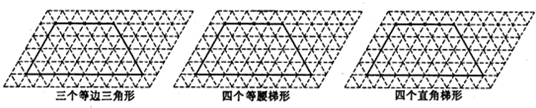
如图所示,在4×4的菱形斜网格图中(每一个小菱形的边长为1,有一个角是60°),菱形ABCD的边长为2,E是AD的中点,按CE将菱形ABCD剪成①、②两部分,用这两部分可以分别拼成直角三角形、等腰梯形、矩形,要求所拼成图形的顶点均落在格点上.
1.(1)在下面的菱形斜网格中画出示意图;
 |
2.
|
|
面积关系是 ;
周长关系是 .
查看答案和解析>>
科目:初中数学 来源:2011年浙江省宁波市外贸学校中考模拟数学卷 题型:解答题
如图所示,在4×4的菱形斜网格图中(每一个小菱形的边长为1,有一个角是60°),菱形ABCD的边长为2,E是AD的中点,按CE将菱形ABCD剪成①、②两部分,用这两部分可以分别拼成直角三角形、等腰梯形、矩形,要求所拼成图形的顶点均落在格点上.
1.(1)在下面的菱形斜网格中画出示意图;
 |
2.
|
|
 )、周长(
)、周长( )的大小关系(用“=”、“>”或“<”连接):
)的大小关系(用“=”、“>”或“<”连接):
面积关系是 ;
周长关系是 .
查看答案和解析>>
科目:初中数学 来源:2010年中考数学模拟试卷5 (解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com