
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求轿车从甲地出发后多长时间再与货车相遇(结果精确到0.01).
解:(1)根据图象信息:货车的速度V货= =60(千米/时)。
=60(千米/时)。
∵轿车到达乙地的时间为货车出发后4.5小时,
∴轿车到达乙地时,货车行驶的路程为:4.5×60=270(千米)。
此时,货车距乙地的路程为:300﹣270=30(千米)。
答:轿车到达乙地后,货车距乙地30千米。
(2)设CD段函数解析式为y=kx+b(k≠0)(2.5≤x≤4.5).
∵C(2.5,80),D(4.5,300)在其图象上,
∴ ,解得
,解得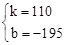 。
。
∴CD段函数解析式:y=110x﹣195(2.5≤x≤4.5);
(3)设轿车从甲地出发x小时后再与货车相遇,
∵V货车=60千米/时, (千米/时),
(千米/时),
∴110(x﹣4.5)+60x=300,解得x≈4.68(小时)。
答:轿车从甲地出发约4.68小时后再与货车相遇。
解析试题分析:(1)根据图象可知货车5小时行驶300千米,由此求出货车的速度为60千米/时,再根据图象得出货车出发后4.5小时轿车到达乙地,由此求出轿车到达乙地时,货车行驶的路程为270千米,而甲、乙两地相距300千米,则此时货车距乙地的路程为:300﹣270=30千米。
(2)设CD段的函数解析式为y=kx+b,将C(2.5,80),D(4.5,300)两点的坐标代入,运用待定系数法即可求解。
(3)设轿车从甲地出发x小时后再与货车相遇,根据轿车(x﹣4.5)小时行驶的路程+货车x小时行驶的路程=300千米列出方程,解方程即可。


科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标中,直角梯形OABC的边OC、OA分别在x轴、y轴上,AB∥OC,∠AOC=900,∠BCO=450,BC= ,点C的坐标为(-18,0).
,点C的坐标为(-18,0).
(1)求点B的坐标;
(2)若直线DE交梯形对角线BO于点D,交y轴于点E,且OE=4,OD=2BD,求直线DE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某社区活动中心为鼓励居民加强体育锻炼,准备购买10副某种品牌的羽毛球拍,每副球拍配x(x≥2)个羽毛球,供社区居民免费借用.该社区附近A、B两家超市都有这种品牌的羽毛球拍和羽毛球出售,且每副球拍的标价均为30元,每个羽毛球的标价为3元,目前两家超市同时在做促销活动:
A超市:所有商品均打九折(按标价的90%)销售;
B超市:买一副羽毛球拍送2个羽毛球.
设在A超市购买羽毛球拍和羽毛球的费用为yA(元),在B超市购买羽毛球拍和羽毛球的费用为yB(元).请解答下列问题:
(1)分别写出yA、yB与x之间的关系式;
(2)若该活动中心只在一家超市购买,你认为在哪家超市购买更划算?
(3)若每副球拍配15个羽毛球,请你帮助该活动中心设计出最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
21.(2013年四川攀枝花8分)某文具店准备购进甲,乙两种铅笔,若购进甲种钢笔100支,乙种铅笔50支,需要1000元,若购进甲种钢笔50支,乙种钢笔30支,需要550元.
(1)求购进甲,乙两种钢笔每支各需多少元?
(2)若该文具店准备拿出1000元全部用来购进这两种钢笔,考虑顾客需求,要求购进甲中钢笔的数量不少于乙种钢笔数量的6倍,且不超过乙种钢笔数量的8倍,那么该文具店共有几种进货方案?
(3)若该文具店销售每支甲种钢笔可获利润2元,销售每支乙种钢笔可获利润3元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知一次函数y=k1x+b(k1≠0)的图象分别与x轴,y轴交于A,B两点,且与反比例函数 (k2≠0)的图象在第一象限的交点为C,过点C作x轴的垂线,垂足为D,若OA=OB=OD=2.
(k2≠0)的图象在第一象限的交点为C,过点C作x轴的垂线,垂足为D,若OA=OB=OD=2.
(1)求一次函数的解析式;
(2)求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年四川广安8分)某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
| | 空调 | 彩电 |
| 进价(元/台) | 5400 | 3500 |
| 售价(元/台) | 6100 | 3900 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
漳州三宝之一“水仙花”畅销全球,某花农要将规格相同的800件水仙花运往A,B,C三地销售,要求运往C地的件数是运往A地件数的3倍,各地的运费如下表所示:
| | A地 | B地 | C地 |
| 运费(元/件) | 20 | 10 | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com