
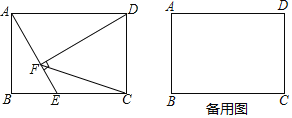
【题目】如图,在矩形ABCD中,AB=4,BC=5,E是BC边上的一个动点,DF⊥AE,垂足为点F,连结CF
(1)若AE=BC
①求证:△ABE≌△DFA;②求四边形CDFE的周长;③求tan∠FCE的值;
(2)探究:当BE为何值时,△CDF是等腰三角形.
【答案】(1)①证明见解析;②12;③![]() ;(2)当BE为3或2.5或2时,△CDF是等腰三角形.
;(2)当BE为3或2.5或2时,△CDF是等腰三角形.
【解析】
(1)①如图1中,根据AAS证明:△ABE≌△DFA即可.
②利用勾股定理求出BE,即可解决问题.
③如图2中,过点F作FM⊥BC于点M.求出FM,MC即可解决问题.
(2)分三种情形分别求解即可解决问题.
解:(1)①如图1中,
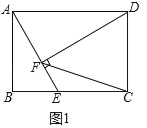
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,∠B=90°,∴∠AEB=∠DAF.
∵DF⊥AE,∴∠AFD=90°.
∴∠B=∠AFD=90°,
又∵AE=BC,
∴AE=AD,
∴△ABE≌△DFA(AAS).
②如图1中,在Rt△ABE中,∠B=90°,
根据勾股定理,得 BE=![]() =3,
=3,
∵△ABE≌△DFA,
∴DF=AB=DC=4,AF=BE=3.
∵AE=BC=5,∴EF=EC=2,
∴四边形CDFE的周长=2(DC+EC)=2×(4+2)=12.
③如图2中,过点F作FM⊥BC于点M.
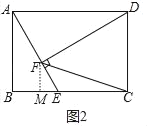
![]() ,
,
在Rt△FME中, ![]() ,
,
![]() ,
,
在Rt△FMC中, ![]() .
.
(2)如图3﹣1中,当DF=DC时,则DF=DC=AB=4.
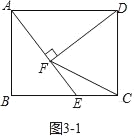
∵∠AEB=∠DAF,∠B=∠AFD=90°,
∴△ABE≌△DFA(AAS).
∴AE=AD=5,
由②可知,BE=3,∴当BE=3时,△CDF是等腰三角形.…
如图3﹣2中,当CF=CD时,过点C作CG⊥DF,垂足为点H,交AD于点G,
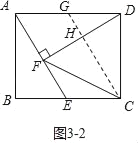
则CG∥AE,DH=FH.
∴AG=GD=2.5.
∵CG∥AE,AG∥EC,
∴四边形AECG是平行四边形,
∴EC=AG=2.5,∴当BE=2.5时,△CDF是等腰三角形.…
如图3﹣中,当FC=FD时,过点F作FQ⊥DC,垂足为点Q.
则AD∥FQ∥BC,DQ=CQ,
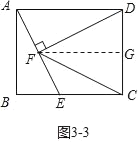
∴AF=FE=![]() AE.
AE.
∵∠B=∠AFD=90°,∠AEB=∠DAF,
∴△ABE∽△DFA,
∴![]() ,即AD×BE=AF×AE.
,即AD×BE=AF×AE.
设BE=x,
∴5x=![]() ,
,
解得x1=2,x2=8(不符合题意,舍去)
∴当BE=2时,△CDF是等腰三角形.
综上所述,当BE为3或2.5或2时,△CDF是等腰三角形.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】某校为了更好地让学生适应中考体育:“1分钟跳绳”项目,对全校九年级200名学生进行了“1分钟跳绳”的测试,现随机抽取20名学生成绩进行分析,过程如下:
收集数据 20名学生的“1分钟跳绳”成绩(单位:个)如下
110 125 134 135 115 146 148 124 153 145
157 160 162 162 165 168 172 128 137 130
整理数据 请你按如下表格分组整理、描述样本数据,并把下列表格补充完整.(说明:每分钟跳绳个数达到160个及以上得满分)
成绩 |
|
|
|
|
|
等级 |
|
|
|
|
|
人数 |
成绩 |
|
|
等级 |
|
|
人数 |
分析数据 请将下列表格补充完整:
平均数 | 中位数 | 满分率 |
143.8 | 30% |
得出结论
(1)用样本中的统计量估计全校九年级学生“1分钟跳绳”等级为__________;
(2)估计该校九年级200名学生中测试“1分钟跳绳”等级为![]() 的人数.
的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
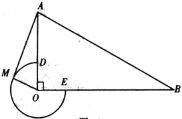
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径作优弧
为半径作优弧![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .点
.点![]() 在优弧
在优弧![]() 上从点
上从点![]() 开始移动,到达点
开始移动,到达点![]() 时停止,连接
时停止,连接![]() .
.
(1)当![]() 时,判断
时,判断![]() 与优弧
与优弧![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)当![]() 时,求点
时,求点![]() 在优弧
在优弧![]() 上移动的路线长及线段
上移动的路线长及线段![]() 的长.
的长.
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
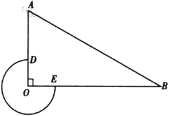
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.

(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
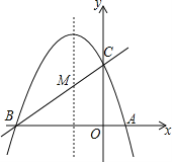
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
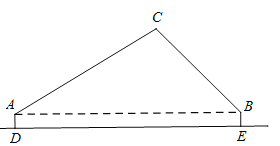
【题目】某数学小组在郊外的水平空地上对无人机进行测高实验.如图,两台测角仪分别放在A、B位置,且离地面高均为1米(即![]() 米),两台测角仪相距50米(即AB=50米).在某一时刻无人机位于点C (点C与点A、B在同一平面内),A处测得其仰角为
米),两台测角仪相距50米(即AB=50米).在某一时刻无人机位于点C (点C与点A、B在同一平面内),A处测得其仰角为![]() ,B处测得其仰角为
,B处测得其仰角为![]() .(参考数据:
.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
(1)求该时刻无人机的离地高度;(单位:米,结果保留整数)
(2)无人机沿水平方向向左飞行2秒后到达点F(点F与点A、B、C在同一平面内),此时于A处测得无人机的仰角为![]() ,求无人机水平飞行的平均速度.(单位:米/秒,结果保留整数)
,求无人机水平飞行的平均速度.(单位:米/秒,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
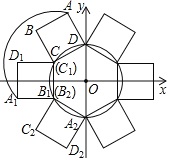
【题目】如图,⊙O的半径为2,圆心O在坐标原点,正方形ABCD的边长为2,点A、B在第二象限,点C、D在⊙O上,且点D的坐标为(0,2),现将正方形ABCD绕点C按逆时针方向旋转150°,点B运动到了⊙O上点B1处,点A、D分别运动到了点A1、D1处,即得到正方形A1B1C1D1(点C1与C重合);再将正方形A1B1C1D1绕点B1按逆时针方向旋转150°,点A1运动到了⊙O上点A2处,点D1、C1分别运动到了点D2、C2处,即得到正方形A2B2C2D2(点B2与B1重合),…,按上述方法旋转2020次后,点A2020的坐标为( )
A.(0,2)B.(2+![]() ,﹣1)
,﹣1)
C.(﹣1﹣![]() ,﹣1﹣
,﹣1﹣![]() )D.(1,﹣2﹣
)D.(1,﹣2﹣![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com