
【题目】如图,矩形![]() 中,AB=8,BC=6,点
中,AB=8,BC=6,点![]() 是射线
是射线![]() 上一动点,设
上一动点,设![]() .过点
.过点![]() 做射线
做射线![]() 的垂线段
的垂线段![]() ,垂足为
,垂足为![]() ,作
,作![]() 的垂直平分线
的垂直平分线![]() 交射线
交射线![]() 于点
于点![]() ,交直线
,交直线![]() 于
于![]() .
.
![]() 点
点![]() 在边
在边![]() 上时.①用含
上时.①用含![]() 的代数式表示
的代数式表示![]() .②当
.②当![]() 时,直线ON交射线CD于
时,直线ON交射线CD于![]() ,求CE的长.
,求CE的长.
![]() 当
当![]() 为何值时,过
为何值时,过![]() 三点的圆与矩形
三点的圆与矩形![]() 的边或对角线
的边或对角线![]() 相切.
相切.
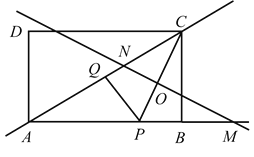
【答案】(1)①![]() ;②
;②![]() (2)当
(2)当![]() 为
为![]() 、
、![]() 或
或![]() 时,过
时,过![]() 、
、![]() 、
、![]() 三点的圆与矩形
三点的圆与矩形![]() 的边或对角线
的边或对角线![]() 相切
相切
【解析】
(1)①现根据勾股定理求得![]() ,然后设
,然后设![]() ,再由余弦函数得到
,再由余弦函数得到![]() ,两式相减即可得到答案;
,两式相减即可得到答案;
②先按比例分配求得![]() ,在由勾股定理求得
,在由勾股定理求得![]() ,然后根据线段垂直平分线的性质、相似三角形的判定和性质即可求得答案;
,然后根据线段垂直平分线的性质、相似三角形的判定和性质即可求得答案;
(2)对过![]() 三点的圆与矩形
三点的圆与矩形![]() 的边或对角线
的边或对角线![]() 相切进行分类讨论,分别画出图形并求得相应的
相切进行分类讨论,分别画出图形并求得相应的![]() 的值即可;
的值即可;
(1)①如图:

由矩形,AB=8,BC=6
可得 ![]()
∵![]() ,
,![]()
∴![]()
∴![]()
②如图:

∵当![]() :
:![]() =3:1时,
=3:1时,![]()
∴![]()
∵![]() 是
是![]() 的垂直平分线
的垂直平分线
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]() 即
即![]()
∴![]() ;
;
(2) Ⅰ) 如图:

当⊙![]() 与边
与边![]() 相切于点
相切于点![]() 时,连结
时,连结![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
Ⅱ) 如图:
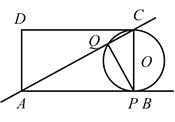
当![]() 与边
与边![]() 相切于点
相切于点![]() 时
时
点![]() 与点
与点![]() 重合,
重合,![]()
Ⅲ) 如图:

当⊙![]() 与对角线
与对角线![]() 相切于点
相切于点![]() 时
时
点![]() 与点
与点![]() 重合,
重合,![]()
∴![]()
∴综上所述,当![]() 为
为![]() 、
、![]() 或
或![]() 时,过
时,过![]() 、
、![]() 、
、![]() 三点的圆与矩形
三点的圆与矩形![]() 的边或对角线
的边或对角线![]() 相切.
相切.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
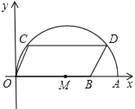
【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C,D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ,
,![]() ,
,![]() .
.
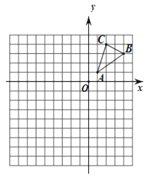
(1)请作出![]() 绕
绕![]() 点逆时针旋转
点逆时针旋转![]() 的
的![]() ;
;
(2)以点![]() 为位似中心,将
为位似中心,将![]() 扩大为原来的2倍,得到
扩大为原来的2倍,得到![]() ,请在
,请在![]() 轴的左侧画出
轴的左侧画出![]() ;
;
(3)请直接写出![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,一架伸缩楼梯托架![]() 固定在墙面上,托架
固定在墙面上,托架![]() 始终与地面垂直且
始终与地面垂直且![]() .如图2, 旋转支撑臂
.如图2, 旋转支撑臂![]() 绕着点
绕着点![]() 旋转,当伸缩楼梯下放时,楼梯长
旋转,当伸缩楼梯下放时,楼梯长![]() 米,点
米,点![]() 正好接触地面,此时,旋转支撑臂
正好接触地面,此时,旋转支撑臂![]() 与楼梯托架
与楼梯托架![]() 之间的夹角为
之间的夹角为![]() ;当伸缩楼梯上收时,旋转支撑臂
;当伸缩楼梯上收时,旋转支撑臂![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() ,楼梯长
,楼梯长![]() 变为
变为![]() 米,此时,楼梯底部的脚垫
米,此时,楼梯底部的脚垫![]() 到地面的距离为( )米.
到地面的距离为( )米.

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)过第二象限的点![]() 作平行于x轴的直线,交直线
作平行于x轴的直线,交直线![]() 于点C,交函数
于点C,交函数![]() 的图象于点D.
的图象于点D.
①当![]() 时,判断线段PD与PC的数量关系,并说明理由;
时,判断线段PD与PC的数量关系,并说明理由;
②若![]() ,结合函数的图象,直接写出n的取值范围.
,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
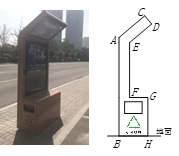
【题目】在太原迎泽西大街上有一种智能垃圾桶,这种智能垃圾桶不仅可以供行人休息,灯箱边的中部还有USB接口可供行人充电.此种垃圾桶的侧面示意图如图所示,其中AC∥ED,AB∥EF∥GH,CD=20cm,DE=60cm,EF=100m,GH=80cm,∠CDE=∠EFG=90°,∠DEF=130°,则此种垃圾桶的高度(C到地面的距离)约为________cm.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com