
【题目】如图,函数y=![]() 和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.
和y= - x+4的图像交点为A、B,原点为O,求△AOB面积.

【答案】8![]()
【解析】整体分析:
联立方程y=![]() 和y= - x+4,求出点A,B的坐标,然后由公式△OAB的面积=
和y= - x+4,求出点A,B的坐标,然后由公式△OAB的面积=![]() ×(x1- x2)(y2- y1)求解.
×(x1- x2)(y2- y1)求解.
解:把y=![]() 代入y= - x+4得,
代入y= - x+4得,
![]() = - x+4,
= - x+4,
解得x1=2+![]() ,x2=2-
,x2=2-![]() .
.
所以y1=2-![]() ,y2=2+
,y2=2+![]() .
.
则A(2-![]() ,2+
,2+![]() ),B(2+
),B(2+![]() ,2-
,2-![]() ),
),
所以△OAB的面积=![]() ×(x1- x2)(y2- y1)==
×(x1- x2)(y2- y1)==![]() ×4
×4![]() ×4
×4![]() =
=![]() .
.
【题型】解答题
【结束】
19
【题目】如图,直线![]() 与双曲线
与双曲线![]() 相交于A(2,1)、B两点.
相交于A(2,1)、B两点.

(1)求m及k的值;
(2)不解关于x、y的方程组 直接写出点B的坐标;
直接写出点B的坐标;
(3)直线![]() 经过点B吗?请说明理由.
经过点B吗?请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
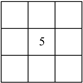
【题目】在如图所示的方格中,填入相应的数字,使它符合下列语句的要求:
(1)5的正上方是一个负整数;
(2)5的左上方是一个正分数;
(3)一个既不是正数也不是负数的数在5的正下方;
(4)5的左边是一个负分数;
(5)剩下的四格请分别填上正数和负数使方格中正数与负数的个数相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【题目】如图,两个反比例函数C1:y=![]() 和C2:y=
和C2:y=![]() 在第一象限内的图象如图,P在C1上作PC、PD垂直于坐标轴,垂线与C2交点为A、B,则下列结论,其中正确的是( )
在第一象限内的图象如图,P在C1上作PC、PD垂直于坐标轴,垂线与C2交点为A、B,则下列结论,其中正确的是( )
①△ODB与△OCA的面积相等;②四边形PAOB的面积等于k1- k2;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点

A. ①② B. ②④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 的图象如右图所示,则结论:
的图象如右图所示,则结论:
①两函数图象的交点![]() 的坐标为
的坐标为![]() ; ②当
; ②当![]() 时,
时, ![]() ;
;
③当![]() 时,
时, ![]() ; ④当
; ④当![]() 逐渐增大时,
逐渐增大时, ![]() 随着
随着![]() 的增大而增大,
的增大而增大, ![]() 随着
随着![]() 的增大而减小.
的增大而减小.
其中正确结论的序号是 .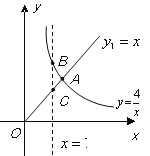
【答案】①③④
【解析】试题分析:反比例函数与一次函数的交点问题.运用一次函数和反比例函数的性质来解决的一道常见的数形结合的函数试题.一次函数和反比例函数的交点坐标就是一次函数与反比例函数组成的方程组的解.根据k>0确定一次函数和反比例函数在第一象限的图象特征来确定其增减性;根据x=1时求出点B点C的坐标从而求出BC的值;当x=2时两个函数的函数值相等时根据图象求得x>2时y1>y2.
试题解析:①由一次函数与反比例函数的解析式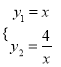 ,
,
解得, ![]() ,
,
∴A(2,2),故①正确;
②由图象得x>2时,y1>y2;故②错误;
③当x=1时,B(1,3),C(1,1),∴BC=3,故③正确;
④一次函数是增函数,y随x的增大而增大,反比例函数k>0,y随x的增大而减小.故④正确.
∴①③④正确.
考点:反比例函数与一次函数的交点问题.
【题型】填空题
【结束】
15
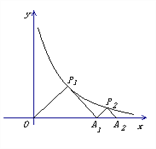
【题目】如图, △P1OA1与△P2A1A2是等腰直角三角形,点![]() 、
、![]() 在函数
在函数![]() 的图象上,斜边
的图象上,斜边![]() 、
、![]() 都在
都在![]() 轴上,则点
轴上,则点![]() 的坐标是____________.
的坐标是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上点A表示数a,点B表示数b,点C表示数c,b是最小的正整数,且a,c满足|a+2|+(c-7)2=0.
(1)填空:a=________,b=________,c=________;
(2)画出数轴,并把A,B,C三点表示在数轴上;
(3)P是数轴上任意一点,点P表示的数是x,当PA+PB+PC=10时,x的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在足球比赛中,甲、乙两名队员互相配合向对方球门MN进攻,当甲带球冲到A点时,乙已跟随冲到B点,如图24-1-4-12.此时,甲自己直接射门好,还是迅速将球传给乙,让乙射门好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个点,且线段AB=4,CD=6,已知A表示的数是﹣10,C表示的数是8,若线段AB以每秒6个单位长度的速度,线段CD以每秒2个单位长度的速度在数轴上运动(A在B左侧,C在D左侧)
(1)B,D两点所表示的数分别是 、 ;
(2)若线段AB向右运动,同时线段CD向左运动,经过多少秒时,BC=2;
(3)若线段AB、CD同时向右运动,同时点P从原点出发以每秒1个单位长度的速度向右运动,经过多少秒时,点P到点A,C的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数 ![]() 是关于x的二次函数,求:
是关于x的二次函数,求:
(1)满足条件的m的值;
(2)m为何值时,抛物线有最低点?求出这个最低点,当x为何值时,y随x的增大而增大;
(3)m为何值时,抛物线有最大值?最大值是多少?当x为何值时,y随x的增大而减小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com