
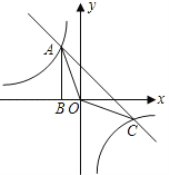
【题目】如图,Rt△ABO的顶点A是双曲线y1=![]() 与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=![]() .
.
(1)求这两个函数的解析式;
(2)求△AOC的面积.
(3)直接写出使y1>y2成立的x的取值范围
【答案】(1)y=﹣![]() ,y=﹣x+2;(2)4;(3)-1<x<0或x>3
,y=﹣x+2;(2)4;(3)-1<x<0或x>3
【解析】(1)欲求这两个函数的解析式,关键求k值.根据反比例函数性质,k绝对值为3且为负数,由此即可求出k;
(2)由函数的解析式组成方程组,解之求得A、C的坐标,然后根据S△AOC=S△ODA+S△ODC即可求出;
(3)根据图象即可求得.
解:(1)设A点坐标为(x,y),且x<0,y>0,
则S△ABO=![]() |BO||BA|=
|BO||BA|=![]() (﹣x)y=
(﹣x)y=![]() ,
,
∴xy=﹣3,
又∵y=![]() ,
,
即xy=k,
∴k=﹣3.
∴所求的两个函数的解析式分别为y=﹣![]() ,y=﹣x+2;
,y=﹣x+2;
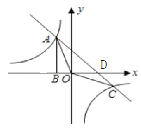
(2)由y=﹣x+2,
令x=0,得y=2.
∴直线y=﹣x+2与y轴的交点D的坐标为(0,2),
∵A、C在反比例函数的图象上,
∴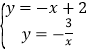 ,
,
解得![]() ,
,![]() ,
,
∴交点A(﹣1,3),C为(3,﹣1),
∴S△AOC=S△ODA+S△ODC=![]() OD(|x1|+|x2|)=
OD(|x1|+|x2|)=![]() ×2×(3+1)=4.
×2×(3+1)=4.
(3)-1<x<0或x>3 .


科目:初中数学 来源: 题型:
【题目】已知A、B两地相距50单位长度。小李从A地出发去B地,以每分钟2单位长度的速度行进,第一次他向左1单位长度,第二次他向右2单位长度,第三次再向左3单位长度,第四次又向右4单位长度,……,按此规律行进,如果A地在数轴上表示的数为-16.
(1)B地在数轴上表示的数为________________。
(2)若B地在原点的右侧,经过第八次进行后,小李到达点P,此时点P与点B相距_____________单位长度,八次运动完成后一共经过__________分钟。
(3)若经过n次(n为正整数)行进后,小李到达点Q,在数轴上点Q表示的数如何表示?(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点. 
(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,当PA+PB最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时。其它主要参考数据如下:
运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费用(元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
(1)如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.
(2)如果A市与某市之间的距离为S千米,且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,你若是某市水果批发部门的经理,要将这种水果从A市运往本市销售。你将选择哪种运输方式比较合算呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1 , 将C1向右平移得C2 , C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( ) 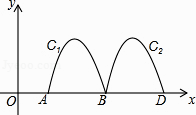
A.﹣2<m< ![]()
B.﹣3<m<﹣ ![]()
C.﹣3<m<﹣2
D.﹣3<m<﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:
①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2;④不等式kx+b>0的解集是x>2.
其中说法正确的有_________(把你认为说法正确的序号都填上).
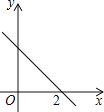
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知|a+3|与(b+1)2互为相反数,a、b分别对应数轴上的点A、B.
(1)求a、b的值.
(2)数轴上原点右侧存在点C,设甲、乙、丙三个动点分别从A、B、C三点同时运动,甲、乙向数轴正方向运动,丙向数轴负方向运动,甲、乙、丙运动速度分别为1、![]() 、2(单位长度每秒),若它们在数轴上某处相遇,请求出C点对应的数是多少?
、2(单位长度每秒),若它们在数轴上某处相遇,请求出C点对应的数是多少?
(3)运用(2)中所求C点对应的数,若甲、乙、丙出发地及速度大小均不变,同时向数轴负方向运动,问丙先追上谁?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为3.6米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.6米,看台最低点A与旗杆底端D之间的距离为16米(C,A,D在同一条直线上).
(1)求看台最低点A到最高点B的坡面距离;
(2)一面红旗挂在旗杆上,固定红旗的上下两个挂钩G、H之间的距离为1.2米,下端挂钩H与地面的距离为1米,要求用30秒的时间将红旗升到旗杆的顶端,求红旗升起的平均速度(计算结果保留两位小数)(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com