Question

20．某公司生产一种新型生物医药产品，生产成本为2万元/吨，每月生产能力为12吨，且生产出的产品都能销售出去．这种产品部分内销部分外销（出口），内销与外销的单价（单位：万元/吨）与销量的关系分别如图1，图2．

（1）如果该公司内销数量为x（单位：吨），内、外销单价分别为y₁，y₂，求y₁，y₂关于x的函数解析式；
（2）如果该公司内销数量为x（单位：吨），求内销获得的毛利润s₁关于x的函数解析式；
（3）请设计一种销售方案，使该公司本月能获得最大毛利润，并求出毛利润的最大值．（毛利润=销售收入-生产成本）．

Answer 1

分析 （1）分0≤x≤4、4＜x≤12两种情况，利用待定系数法即可求得；
（2）利用“总利润=每吨的利润×销售量”分0≤x≤4、4＜x≤12两种情况求解可得；
（3）设内销产品x吨，则外销产品（12-x）吨，设外销毛利润为s₂万元，总利润为s万元，先根据（2）中相等关系列出s₂的函数解析式，在分情况由s=s₁+s₂求得函数解析式，依据二次函数性质求函数的最值即可得．

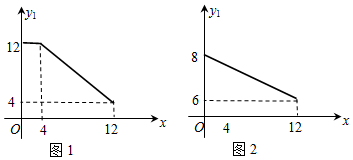
解答 解：（1）当0≤x≤4时，y₁=12，
当4＜x≤12时，设内销单价y₁与x的函数关系为y₁=kx+b，
将（4，12）、（12，4）代入得：$\left\{\begin{array}{l}{4k+b=12}\\{12k+b=4}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-1}\\{b=16}\end{array}\right.$，
∴y₁=-x+16，
即y₁=$\left\{\begin{array}{l}{12}&{（0≤x≤4）}\\{-x+16}&{（4＜x≤12）}\end{array}\right.$；
设外销单价y₂与x的函数关系为y₂=mx+n，
将（0，8）、（12，6）代入，得：$\left\{\begin{array}{l}{n=8}\\{12m+n=6}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{m=-\frac{1}{6}}\\{n=8}\end{array}\right.$，
∴y₂=-$\frac{1}{6}$x+8（0≤x≤12）；

（2）当0≤x≤4时，s₁=（y₁-2）x=10x；
当4＜x≤12时，s₁=（y₁-2）x=（-x+16-2）x=-x²+14x；
即s₁=$\left\{\begin{array}{l}{10x}&{（0≤x≤4）}\\{-{x}^{2}}&{（4＜x≤12）}\end{array}\right.$；

（3）设内销产品x吨，则外销产品（12-x）吨，设外销毛利润为s₂万元，总利润为s万元，
则：s₂=（12-x）[-$\frac{1}{6}$（12-x）+8-2]=-$\frac{1}{6}$x²-2x+48，
当0≤x≤4时，s=s₁+s₂=10x-$\frac{1}{6}$x²-2x+48=-$\frac{1}{6}$x²+8x+48=-$\frac{1}{6}$（x-24）²+144，
∵x＜24时，s随x的增大而增大，
∴当x=4时，s取得最大值，最大值为$\frac{232}{3}$；
当4＜x≤12时，s=s₁+s₂=-x²+14x-$\frac{1}{6}$x²-2x+48=-$\frac{7}{6}$（x-$\frac{36}{7}$）²+$\frac{552}{7}$，
∴当x=$\frac{36}{7}$时，s取得最大值$\frac{552}{7}$，
∵$\frac{552}{7}$＞$\frac{232}{3}$，
综上所述，当x=$\frac{36}{7}$时，s有最大值$\frac{552}{7}$．
即：当安排内销$\frac{36}{7}$吨，外销$\frac{48}{7}$吨时，该公司本月可以获得最大毛利润$\frac{552}{7}$万元．

点评 本题主要考查二次函数的应用，熟练掌握分类讨论思想及依据相等关系列出函数解析式、二次函数的性质求函数的最值是解题的关键．