练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．某商店经营一种小商品，进价是2.5元，据市场调查，销售价是13.5元时，平均每天销售是500件，而销售价每降低1元，平均每天就可以多售出100件．
    （I）假定每件商品降价x元，商店每天销售这种小商品的利润是 y元，请写出y与x间的函数关系式；
    （II）每件小商品销售价是多少元时，商店每天销售这种小商品的利润最大？最大利润是多少？

    分析 （1）根据总利润=（实际售价-进价）×销售量，即可得函数解析式；
    （2）将（1）中函数解析式配方结合x的取值范围即可得最值情况．

    解答 解：（1）设降价x元时利润为y元，
    依题意：y=（13.5-x-2.5）（500+100x）=-100x2+600x+5500；

    （2）∵y=-100x2+600x+5500=-100（x-3）2+6400（0≤x≤11）；
    ∵a=-100＜0，
    ∴当x=3时y取最大值，最大值是6400，即降价3元时利润最大，
    ∴销售单价为10.5元时，最大利润6400元．
    答：销售单价为10.5元时利润最大，最大利润为6400元．

    点评 本题主要考查二次函数的应用，理解题意找到题目蕴含的相等关系列出函数解析式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．如图，AB⊥BC，DC⊥BC，AB=6，BC=14，CD=4，点P是边BC上的一点，连接AP，过点B作BE⊥AP，垂足为E．
    （1）当点P在边BC上移动时（点P不与点B重合），AE•AP的值是否发生变化？若不变，求出这个值；若变化，说明理由；
    （2）当点P移动到BC的中点时，连接AC、BC，求证：∠PAC=∠PCE；
    （3）点P在BC上移动，当以P、C、D为顶点的三角形与△PAB相似时，求PB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．探究：如图①，在矩形ABCD中，AB=3，AD=4，点P是对角线AC上的一点，过点P分别作AB、AD的平行线，交BC、CD于点M、N，求$\frac{PM}{PN}$的值；
    应用：如图②，在矩形ABCD中，AB=3，AD=4，点P是对角线AC上的一点，Rt△PEF的两条直角边PE、PF分别交BC、CD于点M、N，则$\frac{PM}{PN}$=$\frac{3}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．单项式-$\frac{2{x}^{2}{y}^{5}}{7}$的系数是m，次数是n，则m+n=$\frac{33}{7}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

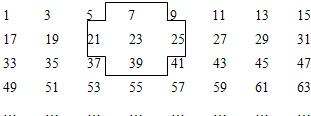    7．将连续的奇数1、3、5、7、9、…排成如图的数表：
    （1）十字框的5个数的和与中间的数23有什么关系？若将十字框上下左右平移，可框住另外5个数，这5个数还有这种规律吗？
    （2）设十字框中中间的数为a，用含a的式子表示十字框中的5个数之和；
    （3）十字框中的5个数的和能等于2016吗？若能，请写出这5个数，若不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．若代数式3xmy2与-2x3yn是同类项，则m-n=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．求下列各式中x的值．
    （1）x2-2=0                              
    （2）（x+1）2-9=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图：已知，△ABC中，∠ABC=60°，∠C=45°，BD为角平分线，矩形DEFG的顶点E在AB上，边FG在BC上，CG=2
    （1）线段BG=2$\sqrt{3}$；
    （2）如图①，请在线段BD和线段BC上分别找一点M、N，使GM+MN最小，并求出GM+MN长度的最小值；
    （3）如图②，连接FD，点O为FD的中点，经过点O是否存在一条直线l，分别交线段AB和BC于点P、Q，并且使△PBQ的面积最小？若存在，请画出这条直线，并求出△PBQ面积的最小值和线段PQ的长度；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算题
    （1）（-8$\frac{3}{7}$）+（-7.5）+（-21$\frac{4}{7}$）+（+3$\frac{1}{2}$）
    （2）（-81）÷$\frac{9}{4}$×$\frac{4}{9}$÷（-16）
    （3）（-24）×（$\frac{1}{3}$-$\frac{1}{8}$-$\frac{1}{6}$）
    （4）-12+[-4+（1-0.2×$\frac{1}{5}$）]÷（-2）2
    （5）-|-$\frac{2}{3}$|-|-$\frac{1}{2}$×$\frac{2}{3}$|-|$\frac{1}{3}$-$\frac{1}{4}$|-|-3|
    （6）-22+（-0.5）2÷（-1$\frac{1}{4}$）-（-2）2×（-$\frac{1}{4}$）
    （7）（-1）2003+（-32）×|-$\frac{2}{9}$|-42÷（-2）2．

    查看答案和解析>>

    同步练习册答案