
【题目】如图,已知△ABC是面积为4![]() 的等边三角形,△ABC∽△ADE,
的等边三角形,△ABC∽△ADE,
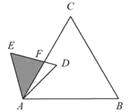
AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积
等于___(结果保留根号).
【答案】3-![]()
【解析】
根据相似三角形面积比等于相似比的平方求得三角形ADE的面积,然后求出其边长,过点F作FH⊥AE,过C作CM⊥AB,利用三角函数求出HF的值,即可得出三角形AFE的面积.
解:作CM⊥AB于M,
∵等边△ABC的面积是4![]() ,
,
∴设BM=x,∴tan∠BCM=![]() ,
,
∴BM=![]() CM,
CM,
∴![]() ×CM×AB=
×CM×AB=![]() ×2×
×2×![]() CM2=4
CM2=4![]() ,
,
∴CM=2![]() ,BM=2,
,BM=2,
∴AB=4,AD=![]() AB=2,
AB=2,
在△EAD中,作HF⊥AE交AE于H,

则∠AFH=45°,∠EFH=30°,
∴AH=HF,
设AH=HF=x,则EH=xtan30°=![]() x.
x.
又∵AH+EH=AE=AD=2,
∴x+![]() x=2,
x=2,
解得x=3-![]() .
.
∴S△AEF=![]() ×2×(3-
×2×(3-![]() )=3-
)=3-![]() .
.
故答案为:3-![]()


科目:初中数学 来源: 题型:
【题目】元旦放假时,小明一家三口一起乘小轿车去探望爷爷、奶奶和姥爷、姥姥.早上从家里出发,向东走了5千米到超市买东西,然后又向东走了2.5千米到爷爷家,下午从爷爷家出发向西走了10千米到姥爷家,晚上返回家里.
(1)若以小明家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和姥爷家的位置在下面数轴上分别用点A、B、C表示出来;
![]()
(2)超市和姥爷家相距多少千米?
(3)若小轿车每千米耗油0.08升,求小明一家从出发到返回家,小轿车的耗油量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“姹紫嫣红苗木种植基地”尝试用单价随天数而变化的销售模式销售某种果苗,利用30天时间销售一种成本为10元/株的果苗,售后经过统计得到此果苗,单价在第x天(x为整数)销售的相关信息,如下图表所示:
销售量n(株) |
|
销售单价 m(元/株) | 当1≤x≤20时,m=________ |
当21≤x≤30时, |
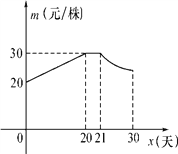
(1)①请将表中当1≤x≤20时,m与x间关系式补充完整;
②计算第几天该果苗单价为25元/株?
(2)求该基地销售这种果苗30天里每天所获利润y(元)关于x(天)的函数关系式;
(3)“吃水不忘挖井人”,为回馈本地居民,基地负责人决定将这30天中,其中获利最多的那天的利润全部捐出,进行“精准扶贫”。试问:基地负责人这次为“精准扶贫”捐赠多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC中,∠C=90°,AB=15,BC=9,点D,E分别在AC,BC上,CD=4 x,CE=3x,其中0<x<3.
(1)求证:DE∥AB;
(2)当x=1时 ,求点E到AB的距离;
(3) 将△DCE绕点E逆时针方向旋转,使得点D落在AB边上的D′处. 在旋转的过程中,若点D′的位置有且只有一个,求x的取值范围.
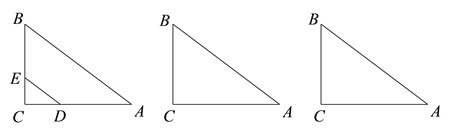
图1 备用图1 备用图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加某体育项目训练,为了便于研究,把最后5次的训练成绩分别用实线和虚线连接起来,如图,下面的结论错误的是( )
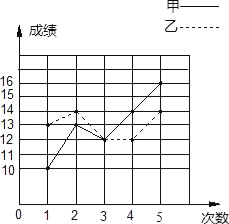
A. 乙的第2次成绩与第5次成绩相同
B. 第3次测试,甲的成绩与乙的成绩相同
C. 第4次测试,甲的成绩比乙的成绩多2分
D. 在5次测试中,甲的成绩都比乙的成绩高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为1,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
(1)求证:四边形PMAN是正方形;
(2)求证:EM=BN;
(3)若点P在线段AC上移动,其他不变,设PC=x,AE=y,求y关于x的解析式,并写出自变量x的取值范围.
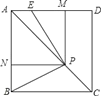
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为![]() ,十位上和个位上的数字之和为
,十位上和个位上的数字之和为![]() ,如果
,如果![]() ,那么称这个四位数为“和平数”.例如:1423,
,那么称这个四位数为“和平数”.例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是_________________,最大的“和平数”是_______________;
(2)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com