练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．三边长均为整数，且最大边长为15的三角形共有（　　）个．
    A．64B．60C．55D．49

    分析 根据三角形的特性：三角形任意两边长之和大于第三边列举解答即可．

    解答 解：若最短边是2，则另一边只能是14，有1个；
    若最短边是3，则另一边可以是13或14，有2个；
    依此类推…
    若最短边是8，则另一边可以是8～14，有7个；
    若最短边是9，则另一边可以是9～14，有6个；
    依此类推…
    若最短边是14，则另一边只能是14，有1个；
    所以有：1+2+…+7+6+…+1=49个三角形满足要求．
    答：三边长为整数，且最大边长为15的三角形一共有49个．
    故选D

    点评 本题考查了图形的计数问题，重点是先确定最短边的长度，然后运用列举的方法分别计数即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    9．如图，点A、B、C是⊙O上的三点，若∠BAC=50°，则∠OBC的度数是（　　）
    A．25°B．40°C．50°D．80°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．如图，甲、乙两所学校，其中男女生情况可见下列统计图，甲学校有1000人，乙有1250人，则（　　）
    A．甲校的女生比乙校的女生多B．甲校的女生比乙校的女生少
    C．甲校与乙校的女生一样多D．甲校与乙校男生共是2250人

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．等边△ABC的边长为3，在边AC上取点A1，使AA1=1，连接A1B，以A1B为一边作等边△A1BC1，则线段AC1的长为2或$\sqrt{13}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

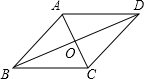    14．如图，四边形ABCD的对角线互相平分，若添加下列条件之一，不能使它变为菱形的条件是（　　）
    A．AB=ADB．AC=BDC．BD平分∠ABCD．AC⊥BD

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．若反比例函数y=-$\frac{4}{x}$的图象经过第二象限的点（a，-a），则a的值为（　　）
    A．2或-2B．-2C．2D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

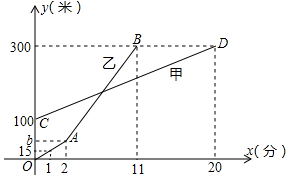    11．甲乙两人同时登同一座山，两人距地面的高度y（米）与登山时间x（分）之间的函数图象如图所示则当乙追上甲时，乙距A地的高度为（　　）
    A．165mB．160mC．135mD．120m

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．对于二次函数y=a（x-h）2+k，对称轴是x=h，顶点坐标是（h，k）．
    （1）当a＞0时，图象开口向上，在对称轴左侧，y随x的增大而减小；在对称轴右侧，y随x的增大而增大，当x=h时，y有最大值，是k；
    （2）当a＜0时，图象开口向下，在对称轴左侧，y随x的增大而增大；在对称轴右侧，y随x的增大而减小，当x=时，y有最小值，是k．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．（1）先化简，再求值：$\frac{{x}^{2}-1}{{x}^{2}-x}$÷（2+$\frac{{x}^{2}+1}{x}$）
    （2）若一次函数y=kx+b经过点A（3，4）、B（4，5），求这一次函数的解析式．

    查看答案和解析>>

    同步练习册答案