
【题目】阅读材料,解决问题
材料一:《孟子》中记载有一尺之棰,日取其半,万世不竭,其中蕴含了“有限”与“无限”的关系.如果我们要计算到第n天时,累积取走了多长的木棒?可以用下面两种方法去解决:
方法一:第n天,留下了![]() 尺木棒,那么累积取走了
尺木棒,那么累积取走了![]() 尺木棒.
尺木棒.
方法二:第1天取走了![]() 尺木棒,第2天取走了
尺木棒,第2天取走了![]() 尺木棒,……第n天取走了
尺木棒,……第n天取走了![]() 尺木棒,那么累积取走了:
尺木棒,那么累积取走了:![]() 尺木棒.
尺木棒.
设:![]() ……①
……①
由①×![]() 得:
得:![]() ……②
……②
①-②得:![]() 则:
则:![]()
材料二:关于数学家高斯的故事,200多年前,高斯的算术老师提出了下面的问题:1+2+3+…+100=?据说当其他同学忙于把100个数逐项相加时,十岁的高斯却用下面的方法迅速算出了正确的答案:(1+100)+(2+99)+…+(50+51)=101×50=5050.
也可以这样理解:令S=1+2+3+4+…+100 ①,则S=100+99+98+…+3+2+1②
①+②得:2S=(1+100)+(2+99)+(3+98)+…+(100+1)=100×(1+100)
即![]()
请用你学到的方法解决以下问题:
(1)计算:![]() ;
;
(2)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层的2倍,问塔的顶层共有多少盏灯?
(3)某中学“数学社团”开发了一款应用软件,推出了“解数学题获取软件激活码”的活动,某一周,这款软件的激活码为下面数学问题的答案:已知一列数1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,……其中第1项是![]() ,接下来的两项是
,接下来的两项是![]() ,
,![]() ,再接下来的三项是
,再接下来的三项是![]() ,
,![]() ,
,![]() ,以此类推,求满足如下条件的正整数N:
,以此类推,求满足如下条件的正整数N:![]() ,且这一列数前N项和为2的正整数幂,请求出所有满足条件的软件激活码正整数N的值.
,且这一列数前N项和为2的正整数幂,请求出所有满足条件的软件激活码正整数N的值.
【答案】(1)![]() ;(2)塔的顶层共有3盏灯;(3)18或95
;(2)塔的顶层共有3盏灯;(3)18或95
【解析】
(1)根据材料的方法可设S=1+3+9+27+…+3n.则3S=3(1+3+9+27+…+3n),利用![]() 即可解答.
即可解答.
(2)设塔的顶层由x盏灯,根据一座7层塔共挂了381盏灯,可列方程.根据材料的结论即可解答.
(3)由题意求得数列的分n+1组,及前n组和S=2n+1-2-n,及项数为![]() ,由题意可知:2n+1为2的整数幂.只需最后一组将-2-n消去即可,求出n值即可求得N的值
,由题意可知:2n+1为2的整数幂.只需最后一组将-2-n消去即可,求出n值即可求得N的值
解:(1)设S=1+3+9+27+…+3n,则3S=3(1+3+9+27+…+3n)=3+9+27+…+3n+3n+1,
∴3S-S=(3+9+27+…+3n+3n+1)-(1+3+9+27+…+3n),
∴2S=3n+1-1,
![]()
(2)设塔的顶层由x盏灯,依题意得:
x+21x+22x+23x+24x+25x+26x=381
解得:x=3,
答:塔的顶层共有3盏灯.
(3)由题意这列数分n+1组:前n组含有的项数分别为:1,2,3,…,n,最后一组x项,根据材料可知每组和公式,求得前n组每组的和分别为:21-1,22-1,23-1,…,2n-1,
总前n组共有项数为N=1+2+3+…+n=![]()
前n所有项数的和为Sn=21-1+22-1+23-1+…+2n-1=(21+22+23+…+2n)-n=2n+1-2-n,
由题意可知:2n+1为2的整数幂.只需最后一组x项将-2-n消去即可,
则①1+2+(-2-n)=0,解得:n=1,总项数为![]() ,不满足10<N<100,
,不满足10<N<100,
②1+2+4+(-2-n)=0,解得:n=5,总项数为![]() ,满足10<N<100,
,满足10<N<100,
③1+2+4+8+(-2-n)=0,解得:n=13,总项数为![]() ,满足10<N<100,
,满足10<N<100,
④1+2+4+8+16+(-2-n)=0,解得:n=29,总项数为![]() ,不满足10<N<100,
,不满足10<N<100,
∴所有满足条件的软件激活码正整数N的值为:18或95。


科目:初中数学 来源: 题型:
【题目】填空并填写理由:如图,AD∥BE,∠1=∠2,那么∠A与∠E相等吗?请完成解答过程:
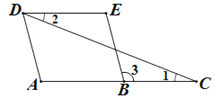
解:∵AD∥BE(已知)
∠A=∠_____ (_________________)
又∵∠1=∠2 (______)
∴AC∥_____ (________________)
∴∠3=∠_____(两直线平行,内错角相等)
∴∠A=∠______ (_______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上,则a的值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量![]() (毫克)随时间
(毫克)随时间![]() (小时)的变化情况如图所示,当成年人按规定剂量服药后.
(小时)的变化情况如图所示,当成年人按规定剂量服药后.

(1)当![]() 时,
时,![]() 与
与![]() 之间的函数关系式是________;
之间的函数关系式是________;
(2)当![]() 时,
时,![]() 与
与![]() 之间的函数关系式是______;
之间的函数关系式是______;
(3)如果每毫升血液中含药量![]() 毫克或
毫克或![]() 毫克以上时,治疗疾病最有效,那么这个有效时间范围是_______小时.
毫克以上时,治疗疾病最有效,那么这个有效时间范围是_______小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一直线上有A、B、C不同三地,甲、乙两人分别从A、B两地同时同向出发前往距离B地150米的C地,甲、乙两人距离B地的距离y(米)与行走试卷x(分)之间的关系图象如图所示,若甲的速度一直保持不变,乙出发2分钟后加速行走,且乙在加速后的速度是甲速度的4倍.
(1)乙加速之后的速度为 米/分;
(2)求当乙追上甲时两人与B地的距离;
(3)当甲出发 分钟时,两人相距10米?
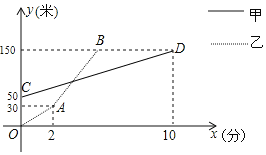
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=80°,求∠BOD的度数;
(2)若∠EOC=∠EOD,求∠BOD的度数.
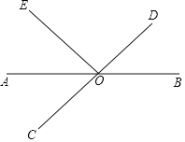
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=-x2+2x,有下列四个结论:①它的对称轴是直线x=1;②设y1=-![]() +2x1,y2=-
+2x1,y2=-![]() +2x2,则当x2>x1时,有y2>y1;③它的图象与x轴的两个交点是(0,0)和(2,0);④当0<x<2时,y>0.其中正确结论的个数为( )
+2x2,则当x2>x1时,有y2>y1;③它的图象与x轴的两个交点是(0,0)和(2,0);④当0<x<2时,y>0.其中正确结论的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com