
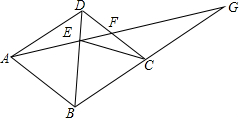
 已知四边形ABCD是菱形,G是BC延长线上一点,AG交BD于点E,交CD于点K,若EF=4,FG=5,求CE的长.
已知四边形ABCD是菱形,G是BC延长线上一点,AG交BD于点E,交CD于点K,若EF=4,FG=5,求CE的长. 分析 根据四边形ABCD是菱形可得出△ADE≌△CDE,则∠DAE=∠DCE,利用平行线的性质得出∠DAE=∠G,进而得出∠G=∠DCE,进而得出△CEF∽△GEC,则EC2=EF•EG,由EF=4,FG=5,从而求出CE.
解答 解:∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDB;
在△ADE和△CDE中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADE=∠CDB}\\{DE=DE}\end{array}\right.$,
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE.
∵AD∥BC,
∴∠DAE=∠G,
∴∠G=∠DCE,
又∵∠CEF=∠GEC,
∴△ECF∽△EGC,
∴EC2=EF•EG,
∵EF=4,FG=5,
∴EG=9,
∴CE=$\sqrt{EF•EG}$=$\sqrt{4×9}$=6.
点评 此题主要考查菱形的性质及相似三角形的判定定理及性质等知识,得出△ECF∽△EGC是解题关键.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 粗心的小马在画数轴时只标注了单位长度(一格表示1个单位长度)和正方向,而忘记了标注原点(如图所示),若点B和点C表示的两个数的绝对值相等,则点A表示的数为-4,点B表示的数为-3,点C表示的数为3.
粗心的小马在画数轴时只标注了单位长度(一格表示1个单位长度)和正方向,而忘记了标注原点(如图所示),若点B和点C表示的两个数的绝对值相等,则点A表示的数为-4,点B表示的数为-3,点C表示的数为3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | xy | B. | y | C. | x | D. | x$\sqrt{y}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com